Матричная модель себестоимости. Планирование затрат производства. Основные уравнения (преобразования стоимости), страница 4

2)  Во втором случае, когда хотя бы одно собственное значение равно единице, определитель матрицы (Е-РР) равен нулю. Как следует из теоремы Кронекера-Капелли [Я.С.Бугров, С.М. Никольский Высшая математика, М. Дрофа, 2003, стр 25], уравнения (1b) или (3b)  имеют бесконечно много решений или не одного. В этом случае производство содержит замкнутый цикл движения стоимости. В частности, выше приведенном примере матрица РР имеет вид

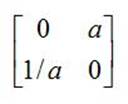
и имеет собственное значение равное единице. В терминах нашей модели, это означает, что мы, (например, при а=2), из одной ложки делаем две вилки, а далее из двух вилок делаем одну ложку. Такое производство может содержать бесконечное число переделов. Производство «ложек-вилок» может также потреблять ресурсы. Производство ложек и вилок  не может повлиять на стоимостные и количественные показатели конечной продукции. По существу два цеха обеспечивают друг друга входными ресурсами, бесследно поглощая выходные ресурсы. Такая матрица норм не может отражать реального производственного процесса (например, потому, что содержит ошибку).

3)   В случае, когда первое (максимальное) собственное значение l меньше единицы, формальное решение существует и является единственным. Итерационное решение представляется бесконечным рядом, сходящимся к точному решению со скоростью геометрической прогрессии с основанием 0<l<1. Оба решения – и итерационное, и формальное - совпадают. 

Следует отметить, что и норма решения уравнения (1b), и норма решения уравнения (3b) пропорциональны величине 1/(1-l). По мере приближения собственного значения l к единице и стоимость полуфабрикатов и их количество стремится к бесконечности.  И неограниченный рост стоимости, и бесконечное число переделов, позволяют заключить, что матрица норм может отражать реальный производственный процесс, однако он организован нерационально. Это может означать также, что матрица норм содержит ошибку.

  Ситуация, когда имеет место бесконечное количество переделов, может быть реализована, например, в кондитерском производстве. При обрезке коржа возникает крошка, которую допускается добавлять в тесто вновь выпекаемых коржей. При этом крошка замещает определенное количество муки, однако стоимость, переносимая крошкой очевидно больше стоимости муки. Это приводит к росту стоимости вновь выпекаемых коржей. Масса крошки может накапливаться до бесконечности. Здесь можно говорить о нерациональной организации производства. При более точном формировании коржей обрезка коржей станет ненужной и стоимость продукции снизится. Если масса обрезаемой крошки очень незначительна по сравнению с массой коржа, то собственное число матрицы РР очень близко к нулю. Бесконечный ряд сходится очень быстро и может быть ограничен первым членом. Вклад крошки в стоимость оказывается незначительным. По мере возрастания доли крошки в формировании коржа  себестоимость его должна расти и при достижении собственным числом единицы стремится к бесконечности. Это будет означать, что сделав корж, потратив на него и материальные и нематериальные (например, трудовые) ресурсы мы превращаем его в крошку и вновь формируем корж. Конечно, при этом и стоимость нематериальных ресурсов будет накапливаться до бесконечности и масса крошки также будет накапливаться до бесконечности.

4)   В случае равенства нулю всех собственных значений формальное решение существует и является единственным. Итерационный процесс представляется конечной суммой, то есть завершается за конечное число итераций, которые моделируют конечное число переделов. Оба решения совпадают. Матрица РР является нильпотентной, то есть  и начиная с некоторой степени для некоторого целого N=0 [Гантмахер Ф.Р. Теория матриц-5-е изданиеМ.:ФИЗМАТЛИТ,2004,стр 201].  Итерационный ряд превращается в конечную сумму. Это означает, что производственный процесс заканчивается за конечное число переделов.

  Для численной реализации существенна оценка числа итераций N. Число итераций строго равно рангу матрицы РР плюс еще одна итерация, расходуемая на вычисление показателей продукции. В свою очередь ранг матрицы не может превышать размерности матрицы РР [Гантмахер Ф.Р. Теория матриц-5-е изданиеМ.:ФИЗМАТЛИТ,2004,стр 12]., то есть числа номенклатурных позиций полуфабрикатов. Поэтому в качестве оценки числа итераций можно использовать число номенклатурных позиций полуфабрикатов, увеличенных на единицу. Внешний вид нильпотентной матрицы  РР  - это треугольная матрица с нулевыми членами на главной диагонали или подобная ей матрица (отличающаяся от треугольной матрицы нумерацией строк и столбцов).