Матричная модель себестоимости. Планирование затрат производства. Основные уравнения (преобразования стоимости), страница 2

 Таким образом, получено обобщение одномерного решения.

2. Учет прямых затрат нематериального характера

Уравнения (1) и (3) позволяют учитывать также расходы и на нематериальные ресурсы, если они допускают нормирование. Предположим, известно, что на единицу каждой номенклатурной позиции продукции расходуется определенное количество человеко-часов труда производственных рабочих, технологов, инженеров. Матрица норм  должна быть расширена на соответствующие  нормы расхода трудовых ресурсов для каждого вида продукции. Вектор цен входных ресурсов  S  следует пополнить почасовыми окладами категорий производственного персонала.  Тогда уравнение (1) даст оценку не только количества сырья, но и необходимых трудовых ресурсов, выраженных в человеко-часах. А уравнение (3) позволит определить себестоимость продукции с учетом расходов на сдельную зарплату.

3. Учет ненормируемых услуг (косвенных затрат)

Примеры ненормируемых услуг, которые трудно наперед отнести к определенной продукции :

- Арендные платежи;

- Оплата энергообеспечения;

- Зарплата администрации;

Эти расходы  следует пропорционально распределить по всей выпускаемой номенклатуре.

В этом случае уравнение баланса (2) принимает вид

 (X,S) + F = (Z,R)   (2')

где F – сумма косвенных затрат.

Очевидно, что с учетом косвенных затрат F решение  (3) преобразуется к виду:

  R = A^TS(1+F/(X,S))   (3')

Вектор решения приобрел безразмерный скалярный сомножитель, увеличивающий себестоимость единицы производимой номенклатуры. Например, если сомножитель составил 1,2 (одну целую две десятых), то себестоимость каждой номенклатурной позиции увеличились на 20%.

4. Многопередельное производство

Здесь мы рассмотрим приложение нашей модели к многопередельному производству, то есть когда для выпуска готовой продукции следует последовательно изготовить целый ряд полуфабрикатов [?].

Наглядным примером многопередельного производства может послужить такая цепочка в кондитерской промышленности:

Входные ресурсы - мука, сахар, масло, сгущенка. Выходные ресурсы –торты.

Первый передел	Корж выпекается из муки Крем готовится из масла и сгущенки
Второй передел	Заготовка торта формируется из коржей и крема
Третий передел	Торт упаковывается в коробку.

Заметим, что многопередельные производственные процессы описываются теми же  уравнениями  (1) и (3). Однако количество и стоимость полуфабрикатов одновременно являются и входящими, и исходящими ресурсами. Следовательно, неизвестные величины, связанные с количеством и стоимостью полуфабрикатов, появляются как в левой, так и в правой частях уравнения.

Систематизируем материальные ресурсы производства.

Входные ресурсы делятся на две группы:

X- вектор потребности в сырье, цены на сырье хранятся в векторе

Y- вектор потребляемых полуфабрикатов, себестоимость полуфабрикатов хранится в векторе P.

Выходные ресурсы также делятся на две группы:

Z- вектор продукции, себестоимость продукции хранится в векторе R,

Y - вектор выпускаемых полуфабрикатов, себестоимость полуфабрикатов хранится в векторе P.

Подчеркнем, что вектор полуфабрикатов Y один и тот же и в группе входных и в группе выходных ресурсов. Мы их выпускаем, чтобы далее потребить.

Такое деление входных и выходных ресурсов приводит к делению матрицы норм на четыре матричных блока:

[RS]- блок преобразования сырья в конечную продукцию,

[PS] - блок преобразования сырья в полуфабрикаты,

[RP]- блок преобразования полуфабрикатов в продукцию,

[PP]-  блок преобразования полуфабрикатов в полуфабрикаты, то есть

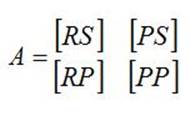
Уравнение потребности ресурсов (1) приобретает вид системы двух векторных уравнений:

(1a) 

 

  (1b)

 

Таким образом, при заданных векторе Z и матрице норм, состоящей из четырех блоков [RS],[PS],[RP] ,[PP], из уравнений (1a) и (1b) следует определить неизвестные вектора X и Y.

Заметим, что теперь стоимость входных ресурсов представляется суммой  (X,S)+(Y,P), а стоимость выходных ресурсов равна  (Z, R)+(Y,P).  Таким образом, уравнение баланса (2) не меняется:

  (X,S)= (Z,R)   (2a)

Уравнение преобразования стоимости (3) приобретает вид системы двух векторных уравнений. Так как транспонирование матрицы, состоящей из матричных блоков, приводит к транспонированию каждого блока и транспонированию блочной структуры, то можно записать: