Заданная система
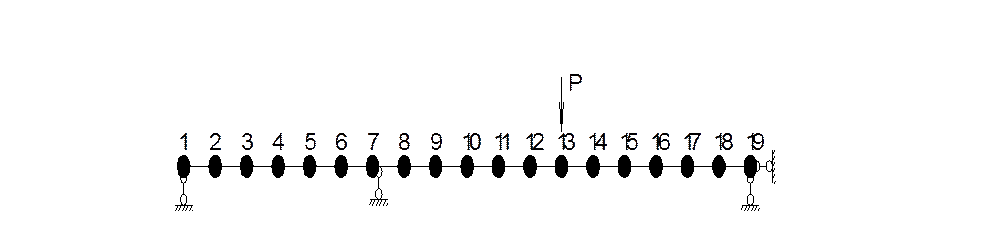
![]() Стационарными,
или установившимися колебаниями упругой системы называются такие движения всех
масс системы, при которых форма изогнутой оси системы, т.е. соотношение между
перемещениями точек, остается постоянной, а сами перемещения изменяются во
времени по единому закону.
Стационарными,
или установившимися колебаниями упругой системы называются такие движения всех
масс системы, при которых форма изогнутой оси системы, т.е. соотношение между
перемещениями точек, остается постоянной, а сами перемещения изменяются во
времени по единому закону.
Если внешним воздействием нарушить состояние устойчивого равновесия механической системы, а затем устранить это внешнее воздействие, то система начнет совершать колебания относительно исходного положения равновесия. Такие колебания называются свободными. Их форма в общем случае нестационарная.
Однако, если надлежащим образом задаться начальным положением системы, то можно получить стационарные свободные колебания. Такие колебания называются собственными.
Определение собственных частот и форм.
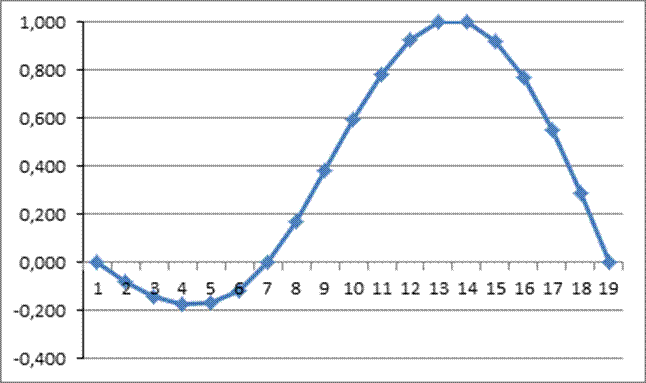
· 1 собственная форма колебаний с частотой SW = 0,0268 Гц
Начальная частота равна 0,015 гц.
Конечная частота – 0,08 гц.
|
№ |
Ux |
Uy |
|
1 |
0 |
0,000 |
|
2 |
0 |
-0,076 |
|
3 |
0 |
-0,138 |
|
4 |
0 |
-0,172 |
|
5 |
0 |
-0,168 |
|
6 |
0 |
-0,114 |
|
7 |
0 |
0,000 |
|
8 |
0 |
0,174 |
|
9 |
0 |
0,384 |
|
10 |
0 |
0,597 |
|
11 |
0 |
0,784 |
|
12 |
0 |
0,924 |
|
13 |
0 |
0,999 |
|
14 |
0 |
1,000 |
|
15 |
0 |
0,922 |
|
16 |
0 |
0,769 |
|
17 |
0 |
0,552 |
|
18 |
0 |
0,288 |
|
19 |
0 |
0,000 |
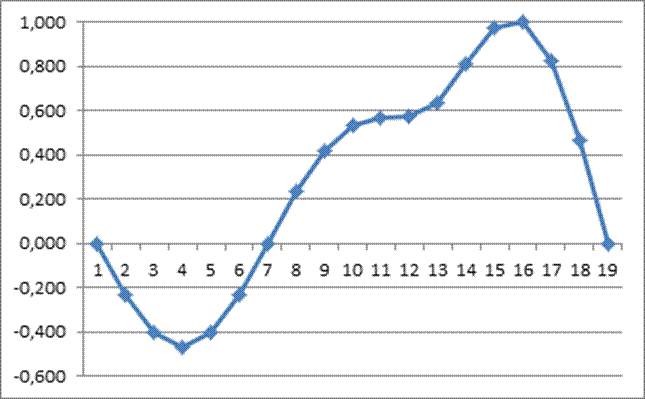
· 2 собственная форма колебаний с частотой SW = 0,0804 Гц
Начальная частота равна 0,0268 гц.
Конечная частота – 0,15 гц.
|
№ |
Ux |
Uy |
|
1 |
0 |
0,000 |
|
2 |
0 |
-0,234 |
|
3 |
0 |
-0,404 |
|
4 |
0 |
-0,467 |
|
5 |
0 |
-0,404 |
|
6 |
0 |
-0,233 |
|
7 |
0 |
0,000 |
|
8 |
0 |
0,235 |
|
9 |
0 |
0,422 |
|
10 |
0 |
0,533 |
|
11 |
0 |
0,571 |
|
12 |
0 |
0,576 |
|
13 |
0 |
0,634 |
|
14 |
0 |
0,810 |
|
15 |
0 |
0,975 |
|
16 |
0 |
1,000 |
|
17 |
0 |
0,826 |
|
18 |
0 |
0,467 |
|
19 |
0 |
0,000 |
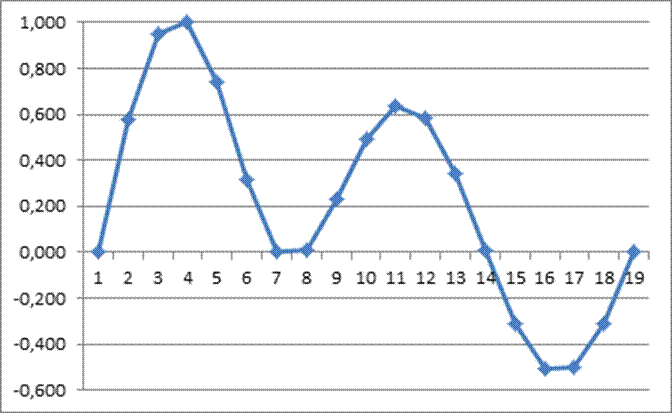
· 3 собственная форма колебаний с частотой SW = 0,1129 Гц
Начальная частота равна 0,0804 гц.
Конечная частота – 0,16 гц.
|
Ux |
Uy |
|
|
1 |
0 |
0,000 |
|
2 |
0 |
0,576 |
|
3 |
0 |
0,950 |
|
4 |
0 |
1,000 |
|
5 |
0 |
0,738 |
|
6 |
0 |
0,318 |
|
7 |
0 |
0,000 |
|
8 |
0 |
0,008 |
|
9 |
0 |
0,234 |
|
10 |
0 |
0,493 |
|
11 |
0 |
0,636 |
|
12 |
0 |
0,582 |
|
13 |
0 |
0,343 |
|
14 |
0 |
0,006 |
|
15 |
0 |
-0,314 |
|
16 |
0 |
-0,507 |
|
17 |
0 |
-0,504 |
|
18 |
0 |
-0,311 |
|
19 |
0 |
0,000 |
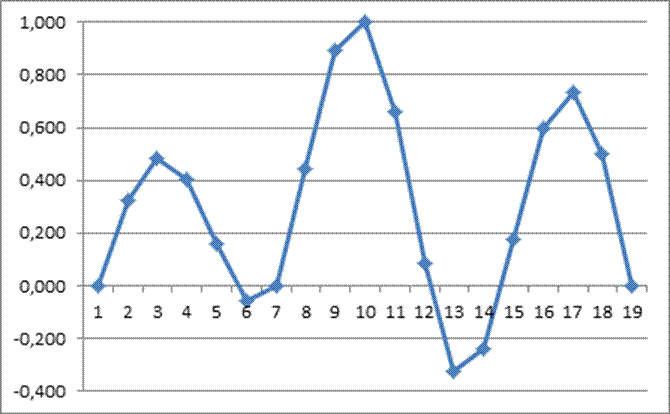
· 4 собственная форма колебаний с частотой SW = 0,1655 Гц
Начальная частота равна 0,1129 гц.
Конечная частота – 0,17 гц.
|
Ux |
Uy |
|
|
1 |
0 |
0,000 |
|
2 |
0 |
0,325 |
|
3 |
0 |
0,483 |
|
4 |
0 |
0,405 |
|
5 |
0 |
0,161 |
|
6 |
0 |
-0,056 |
|
7 |
0 |
0,000 |
|
8 |
0 |
0,443 |
|
9 |
0 |
0,896 |
|
10 |
0 |
1,000 |
|
11 |
0 |
0,661 |
|
12 |
0 |
0,084 |
|
13 |
0 |
-0,328 |
|
14 |
0 |
-0,241 |
|
15 |
0 |
0,178 |
|
16 |
0 |
0,595 |
|
17 |
0 |
0,735 |
|
18 |
0 |
0,498 |
|
19 |
0 |
0,000 |
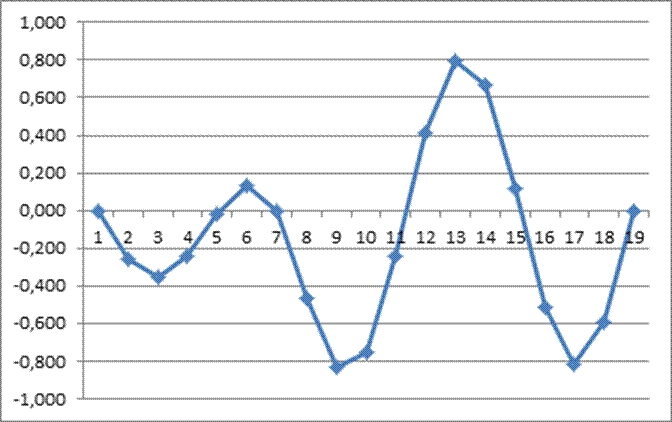
· 5 собственная форма колебаний с частотой SW = 0,1969 Гц
Начальная частота равна 0,1655 гц.
Конечная частота – 0,20 гц.
|
Ux |
Uy |
|
|
1 |
0 |
0,000 |
|
2 |
0 |
-0,255 |
|
3 |
0 |
-0,354 |
|
4 |
0 |
-0,244 |
|
5 |
0 |
-0,017 |
|
6 |
0 |
0,134 |
|
7 |
0 |
0,000 |
|
8 |
0 |
-0,462 |
|
9 |
0 |
-0,829 |
|
10 |
0 |
-0,756 |
|
11 |
0 |
-0,240 |
|
12 |
0 |
0,412 |
|
13 |
0 |
0,794 |
|
14 |
0 |
0,667 |
|
15 |
0 |
0,114 |
|
16 |
0 |
-0,512 |
|
17 |
0 |
-0,813 |
|
18 |
0 |
-0,596 |
|
19 |
0 |
0,000 |
Проверка ортогональности собственных форм
Силы инерции, действующие на массу mi при стационарных колебаниях по k-той собственной форме определяются в виде:
![]()
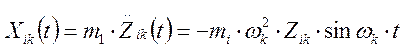
Рассмотрим две собственные формы с номерами 1 и 2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.