I семестр ЛЕКЦИЯ 10
2.6.3 Свойство матрицы жесткости![]()
Задача о вынужденных колебаниях
при гармоническом воздействии сведена к решению алгебраической системы
уравнений относительно амплитудных значений обобщенных координат 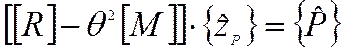 ,
,
т.е., по сути дела, к решению задачи статики с матрицей жесткости, зависящей от распределения масс и от частоты возмущения.
Свойство этой «динамической» матрицы жесткости: После прямого хода при обращении матрицы
по способу Гаусса на главной диагонали появляются отрицательные элементы,
причем количество этих элементов равно номеру участка, которому принадлежит
частота θ . Иными словами,
если на главной диагонали оказалось m отрицательных членов, то частота находится
в интервале ![]() .
.
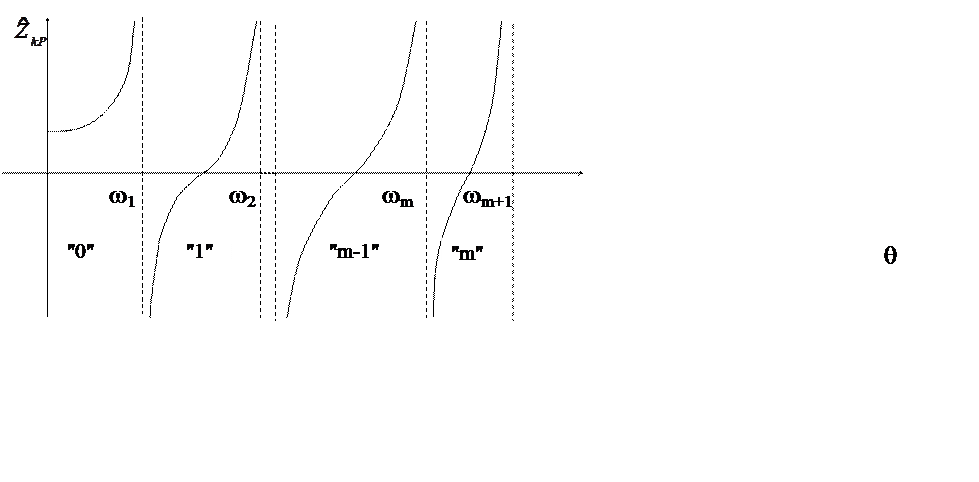 |
На этом свойстве основан изложенный ниже алгоритм определения собственных частот.
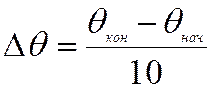 .
.Организуем цикл вычислений:
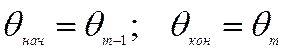 .
.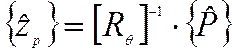 .
.2.6.4 Произвольное динамическое воздействие. Решение разложением по собственным формам.
Этот способ решения дифференциальных уравнений движения основан на свойстве ортогональности собственных форм.
Как и в задаче о свободных колебаниях начнем с уравнений не содержащих слагаемых, которые описывают диссипативные силы
![]() .
.
Считая заранее
определенными собственные формы колебаний (собственные векторы) динамической
системы
![]() , k=1,…,n
, k=1,…,n
будем искать решение в виде суммы
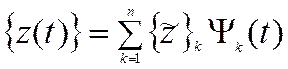 ,
,
где ![]() , k=1,…,n - функции времени.
, k=1,…,n - функции времени.
Заметим, что представление решения в виде суперпозиции собственных форм допустимо только для линейных задач.
Это же выражение, записанное в матричной форме:
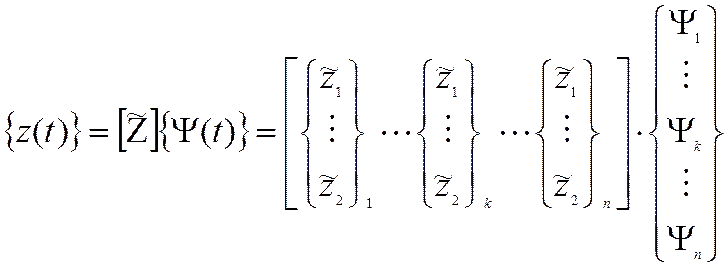 .
.
Тогда матричное уравнение движения принимает вид
![]() .
.
Умножим это уравнение слева на транспонированный столбец ![]() . Получим
. Получим
![]()
или
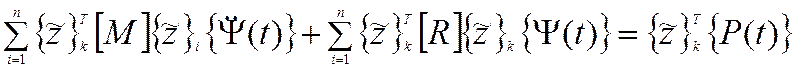 /
/
Благодаря свойству ортогональности собственных форм в левой части равенства останутся только слагаемые с i = k, все остальные равны нулю. Следовательно уравнение примет вид
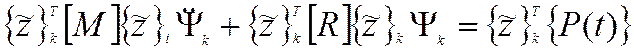 .
.
 |
Напомним вид, который приняло уравнение свободных колебаний при подстановке в него частного решения:
![]() .
.
Заменим
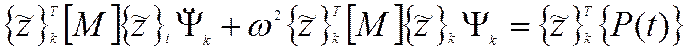 ,
,
или
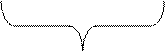

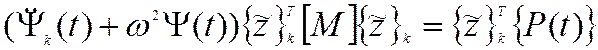 .
.
|
|
|
|
приведенная масса при |
приведенная обобщенная сила при колебаниях по k собственной форме |
Уравнение приобретает вид уравнения вынужденных колебаний системы с одной степенью свободы
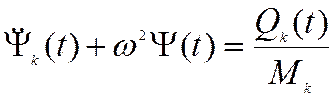 .
.
Учтем, что индекс k пробегает значения от 1 доn: k=1,…, n.
Таким образом, благодаря выбору собственных форм в качестве обобщенных координат, получили вместо системы n дифференциальных уравнений относительно n неизвестных функций n отдельных дифференциальных уравнений, каждое из которых определяет одну неизвестную функцию.
Общее решение k-го уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения:
![]()
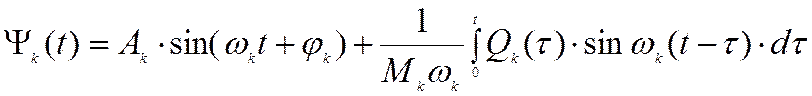 .
.
Решением системы уравнений является сумма решений каждого из уравнений
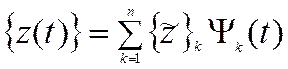 .
.
Неизвестные постоянные
интегрирования ![]() и
и ![]() ,k=1,…,n определяются из начальных условий, которым должно удовлетворять решение
системы уравнений
,k=1,…,n определяются из начальных условий, которым должно удовлетворять решение
системы уравнений ![]() .
.
Выше изложен метод главных или нормальных координат, примененный при решении задачи о вынужденных колебаниях системы при отсутствии диссипации.
В связи с отсутствием надежной исходной информации о распределении сил неупругого сопротивления движению, как правило, оказывается достаточным учесть демпфирование на стадии исследования уже преобразованной системы, вводя в каждое из полученных отдельных уравнений слагаемое, пропорциональное скорости. Результатом этого действия станет появление в решении множителя в виде возведенного в отрицательную степень основания натурального алгоритма и изменением значения собственной частоты:
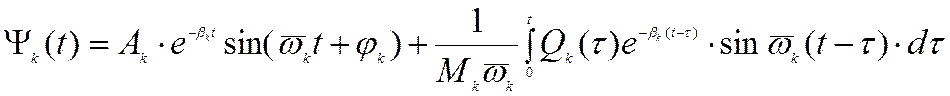 ,
,
где 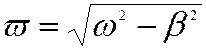 .
.
2.6.5 Произвольное динамическое воздействие. Численное интегрирование.
В тех ситуациях, когда конструкция составлена из разнородных материалов, обладающих резко различными диссипативными свойствами, а также при наличии в системе конструктивных демпферов, введение независимых сил вязкого сопротивления приводит к существенным ошибкам в результатах. Это особенно отчетливо проявляется при близких к резонансным режимах внешних воздействий, причем демпфирование существенно влияет на формы колебаний системы.
В этом случае следует решение производить с помощью численного интегрирования.
Есть и еще один мотив, подталкивающий к использованию процедур численного интегрирования. Когда внешнее воздействие представляет собой сложную функцию времени, и это возмущение задано на ограниченном временном интервале, инженера может интересовать состояние системы в переходных процессах.
![]() .
.
Решением является столбец ![]()
Весь временной интервал разбивается на малые промежутки ![]() .
.
Столбец скоростей 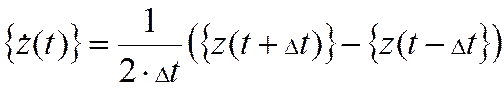 .
.
Столбец ускорений 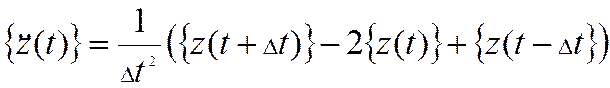 .
.
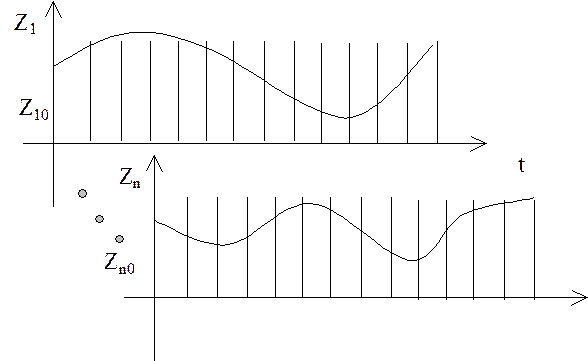 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.