Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра компьютерных систем и программных технологий
Реферат
по Психологии
Жизненные планы
Работу выполнил студент группы №4081/2 Головченко Алексей
Санкт-Петербург
2010
1. Цель работы.
Изучение методов анализа устойчивости замкнутой импульсной системы, исследование влияния изменения параметров системы и шага квантования по времени на динамические свойства системы.
Определение параметров системы с конечным временем переходного процесса.
2. Устойчивость дискретных систем.
Необходимым и достаточным условием асимптотической устойчивости импульсной системы является расположение полюсов передаточной функции системы внутри единичного круга.
При исследовании устойчивости дискретных систем можно использовать критерии, аналогичные критериям для непрерывных систем, но необходимо предварительно преобразовать импульсную передаточную функцию W(z) с помощью подстановки:
![]()
Эта замена в теории функций комплексного переменного также называется билинейным преобразованием.
После замены можно использовать любой из известных критериев устойчивости.
3. Выполнение работы.
3.1. Звено 1.
3.1.1. Расчет дискретной передаточной функции разомкнутой системы.
Заданная передаточная функция непрерывной системы.
![]()
Дискретная передаточная функция системы с идеальным ключом и фиксатором на входе.
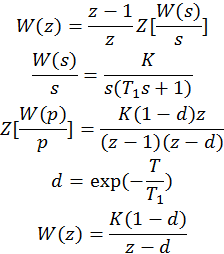
Дискретную передаточную функцию разомкнутой и замкнутой системы можно рассчитать из исходной непрерывной системы используя функции пакета Control System Toolbox Matlab. Пример, расчет дискретной передаточной функции по заданной непрерывной передаточной функции, период дискретизации T = 0.1.
|
Листинг 3.1.1.1. Расчет ДПФ в Matlab. |
|
Wc = tf([1],[1.4 1]) Wd = c2d(Wc, 0.1) % Дискретная ПФ format long; [num_Wd,den_Wd,ts_Wd]=tfdata(Wd); |
С помощью tfdata можно получить численные значения коэффициентов числителя и знаменателя для использования при моделировании системы в Simulink. При подстановке значений в Simulink нужно использовать формат long, так как округление коэффициентов влияет на результат моделирования.
|
Листинг 3.1.1.2. Коэффициенты числителя и знаменателя W(z) |
|
>> num_Wd{1} ans = 0 0.068937220295977 >> den_Wd{1} ans = 1.000000000000000 -0.931062779704023 |
![]()
3.1.2. Расчет дискретной передаточной функции замкнутой системы.
H(z) – передаточная функция замкнутой системы. Рассчитывается аналогично непрерывной системе.
![]()
Передаточную функцию замкнутой системы можно так же рассчитать с помощью Control System Toolbox.
|
Листинг 3.1.2.1. Расчет ДПФ в Matlab. |
|
Hd = feedback(Wd, 1) % Дискретная ПФ замкнутой системы format long; [num_Hd,den_Hd,ts_Hd]=tfdata(Hd); |
3.1.3. Расчет предельного значения K.
Кпред — предельное значение коэффициента усиления разомкнутой системы при котором замкнутая система находится на границе устойчивости.
Сделаем замену переменных (билинейное преобразование) и применим критерий Гурвица. Характеристическое уравнение системы:
![]()
![]() - граница устойчивости.
- граница устойчивости.
![]()
3.1.4. Расчет оптимального значения K.
Копт находится из условия равенства нулю всех коэффициентов знаменателя передаточной функции.
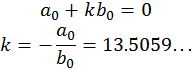
3.1.5. Моделирование системы в Simulink.
Схема моделирования.
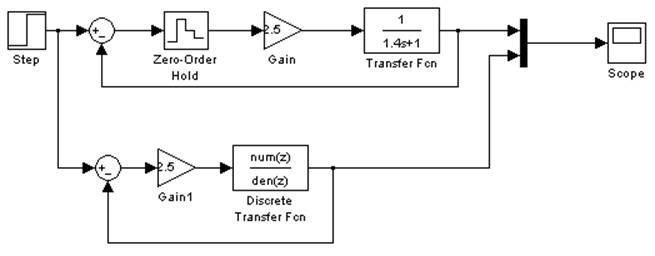
Рис. 3.1.5.1.
Схема моделирования в Simulink.
Переходные характеристики системы при различных коэффициентах усиления.
K = 2.5
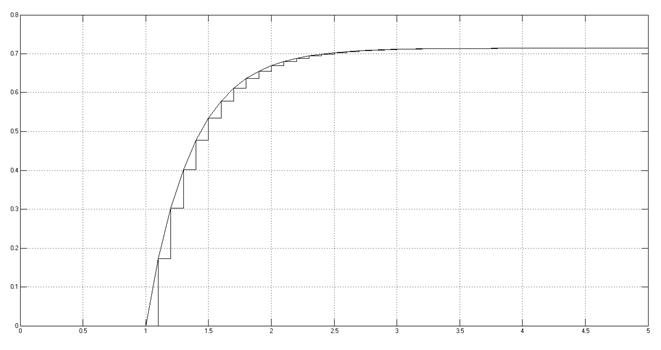
Рис. 3.1.5.1.
Снятая осциллограмма.
K = Kпред.
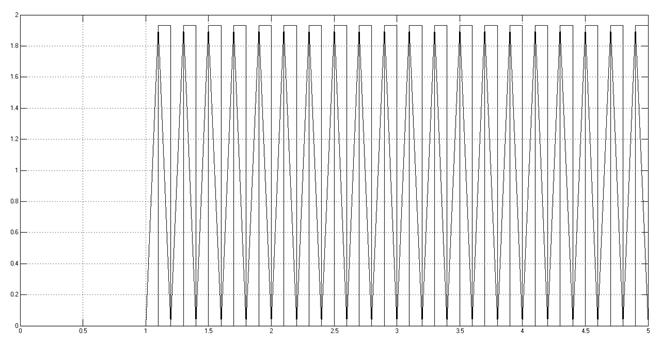
Рис. 3.1.5.2.
Снятая осциллограмма.
К = 0.8 Кпред.
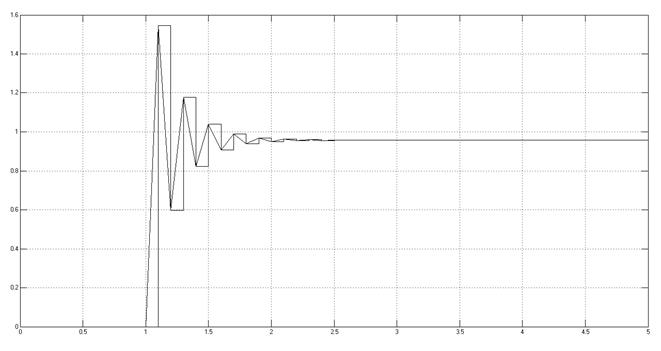
Рис. 3.1.5.3.
Снятая осциллограмма.
К = Копт.
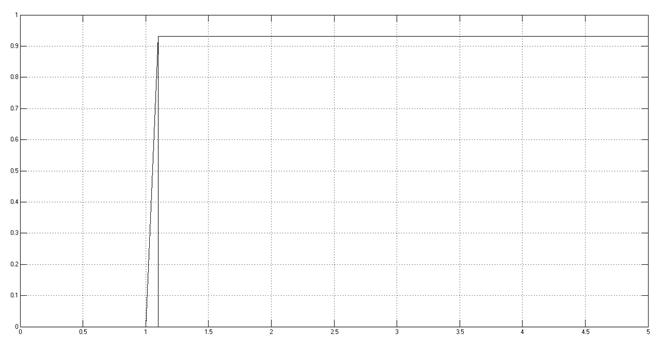
Рис. 3.1.5.4.
Снятая осциллограмма.
При заданном значении значении коэффициента усиления, переходный процесс имеет апериодический характер; при оптимальном значении коэффициента усиления переходный процесс заканчивается за 1 период дискретизации; при увеличении K до Кпред переходный процесс становится колебательным; при K = Кпред в системе существуют незатухающие колебания.
3.1.6. Исследование влияния периода квантования на качество процессов.
Дискретная передаточная функция зависит от значения периода квантования.
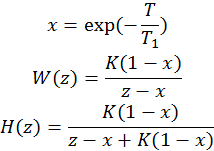
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.