Жизненные планы. Изучение методов анализа устойчивости замкнутой импульсной системы, исследование влияния изменения параметров системы и шага квантования по времени на динамические свойства системы, страница 3

Осциллограмма, полученная при моделировании системы в Simulink.         

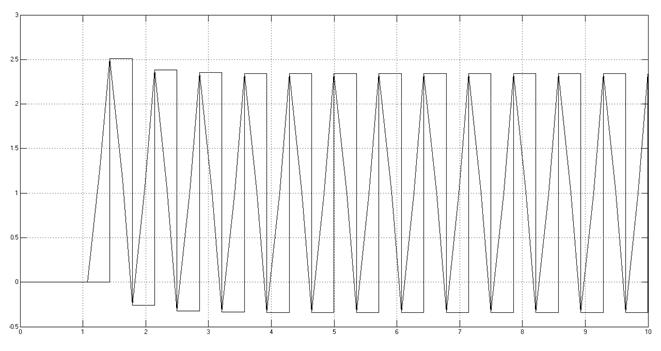
Рис. 3.2.6.1. Снятая осциллограмма.

Увеличение периода квантования влияет на предельное значение коэффициента усиления, соответствующего границе устойчивости. Зависимость Kпред от Т имеет след вид.

Рис.  3.1.6.2. Зависимость Кпред от Т

Видно, что при увеличении периода квантования уменьшается запас устойчивости системы.

Так же, предельное значение периода квантования зависит от постоянной времени системы, чем меньше постоянная времени системы, тем больше предельное значение периода квантования.

3.3. Звено 3.

3.3.1. Расчет дискретной передаточной функции разомкнутой системы.

Заданная передаточная функция непрерывной системы.

Дискретная передаточная функция системы с идеальным ключом и фиксатором на входе.

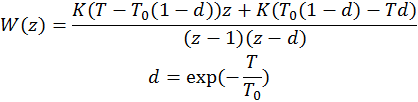
Дискретную передаточную функцию разомкнутой и замкнутой системы можно рассчитать из исходной непрерывной системы используя функции пакета Control System Toolbox Matlab. Пример, расчет дискретной передаточной функции по заданной непрерывной передаточной функции, период дискретизации T = 0.1.

Листинг 3.3.1.1. Расчет ДПФ в Matlab.

Wc = tf([1],[0.9 1 0]) Wd = c2d(Wc, 0.1) format long; [num_Wd,den_Wd,ts_Wd]=tfdata(Wd);

С помощью tfdata можно получить численные значения коэффициентов числителя и знаменателя для использования при моделировании системы в Simulink.

Листинг 3.3.1.2. Коэффициенты числителя и знаменателя W(z)

>> num_Wd{1} ans = 0   0.005355385132933   0.005160683185630 >> den_Wd{1} ans = 1.000000000000000  -1.894839316814370   0.894839316814370

3.3.2. Расчет дискретной передаточной функции замкнутой системы.

H(z) – передаточная функция замкнутой системы. Рассчитывается аналогично непрерывной системе.

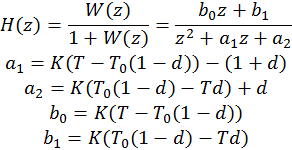
Передаточную функцию замкнутой системы можно так же рассчитать с помощью Control System Toolbox.

Листинг 3.3.2.1. Расчет ДПФ в Matlab.

Hd = feedback(Wd, 1)                   % Дискретная ПФ замкнутой системы format long; [num_Hd,den_Hd,ts_Hd]=tfdata(Hd);

3.3.3. Расчет предельного значения K.

Сделаем замену переменных (билинейное преобразование) и применим критерий Гурвица. Характеристическое уравнение системы:

-  граница устойчивости.

3.3.4. Моделирование системы в Simulink.

Схема моделирования.

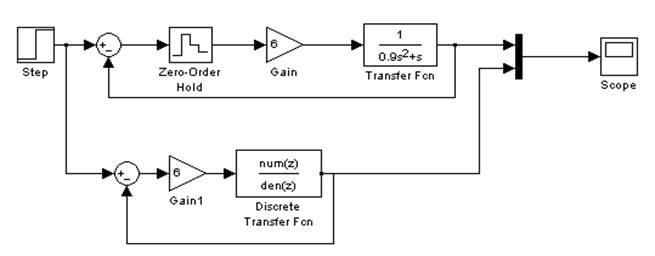
Рис. 3.3.4.1. Схема моделирования в Simulink.

Переходные характеристики системы при различных коэффициентах усиления.

K = 6

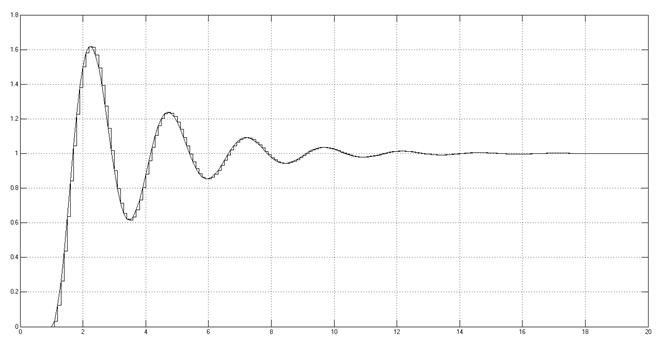
Рис. 3.3.4.2. Снятая осциллограмма.

K = K_пред.

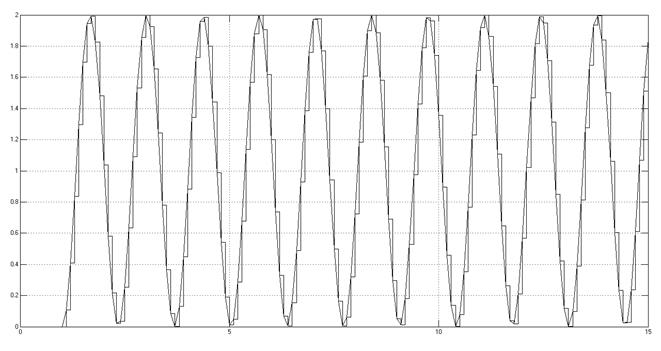
Рис. 3.3.4.3. Снятая осциллограмма.

К = 0.8 К_пред.

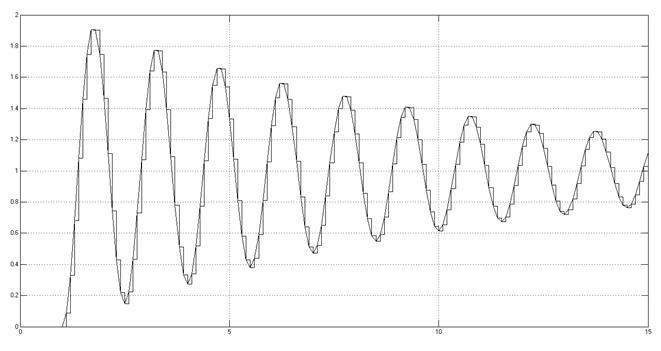
Рис. 3.3.4.4. Снятая осциллограмма.

При заданном значении значении коэффициента усиления, переходный процесс имеет вид затухающих колебаний; при увеличении K до К_пред колебательность переходного процесса увеличивается; при  K = К_пред в системе существуют незатухающие колебания.

3.3.5. Исследование влияния периода квантования на качество процессов.

Предельное значение периода квантования найдем из того же условия, что и предельное значение коэффициента усиления.

-  граница устойчивости.

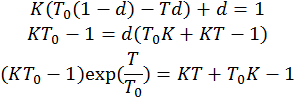
Из последнего уравнения можно найти предельное значение периода квантования. Самый простой способ — приближенно решить уравнение графически. Результат, T примерно 0.357

Результаты моделирования.

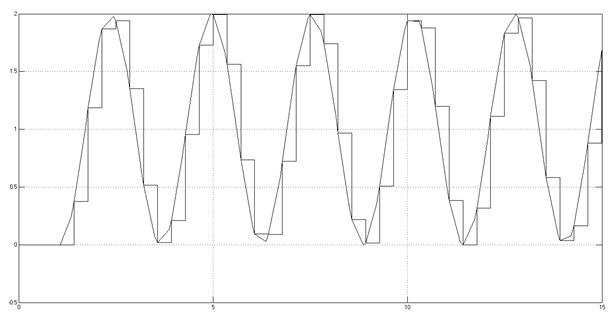
Рис. 3.3.5.1. Снятая осциллограмма.

Предельное значение периода квантования так же как и в предыдущих случаях зависит от коэффициента усиления и постоянной времени звена. Зависимость описывается выведенным из условия границы устойчивости уравнением.

4. Выводы и анализ результатов работы.

Устойчивость и качество переходных процессов в дискретных системах так же как и в непрерывных зависит от параметров звеньев системы (таких как коэффициент усиления и постоянная времени).

Так же на динамические свойства дискретной системы большое влияние оказывает период квантования.

Предельные параметры звеньев и период интегрирования жестко связаны. Изменение периода квантования влияет на запасы устойчивости системы по одному из ее параметров. Например, в рассмотренных первых двух системах при увеличении периода квантования запасы устойчивости системы по коэффициенту усиления уменьшаются.