Процедура формирования матрицы. Норма вектора и матриц

В А Р И А Н Т     N 1

Составить процедуру формирования матрицы  A(N,N) , зависящей от параметра  X

A =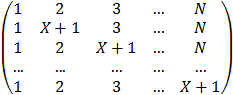

Используя эту процедуру, подпрограммы  DECOMP  и  SOLVE , найти  A^-1  для N=5 и значений X = 1.1 , 1.001 , 1.00001 , для каждого  X  вычислить матрицу R=AA^-1 - E и ее норму.

В А Р И А Н Т     N 2

Написать процедуру формирования матрицы  A  по заданному вектору  B

A = 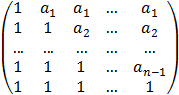,             B = ( a₁ , a₂ , …, a_n-1 )^T

Задавая  n=5 , a₁ = 4 , a₂ = 3 , a₃ = 2 , a₄ = var = 1.5 ; 1.01 ; 1.001 ; 1.0001  и вычисляя  A^-1  с помощью  DECOMP  и  SOLVE  , найти нормы матриц 

R = AA^-1 - E  для всех вариантов  a₄ .

В А Р И А Н Т     N 3

Составить процедуру формирования матрицы  A(N,N) , зависящей от параметра  a

A =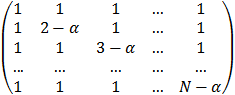

Решить систему  Ay = B , где  B_k = k+cos(k) , используя программы  DECOMP  и  SOLVE , для  a = 0.9999 ; 0.99999 ; 0.999999  и для  N=4. Сравнить результаты решения с двойной и стандартной точностью.

В А Р И А Н Т     N 4

Составить процедуру формирования матрицы  A(e)  по заданному параметру  e

A =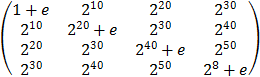

Для  e = 10 , 1 , 0.1  сравнить решения систем  A^TAx=A^Tb  и  Ax=b  для 

b = (1, 2, 3, 4)^T  в этих трех случаях. Сравнение результатов проводить по норме невязок  R = Ax-b  и  R = A^TAx-A^Tb . Норму вектора вычислять по формуле

В А Р И А Н Т     N 5

Составить процедуру вычисления нормы матрицы  R = AA^-1 - E , где

Используя  DECOMP  и  SOLVE , вычислить  A^-1  по заданной матрице 

A =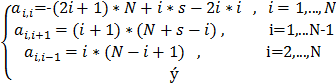

Для N=4 и четырех значений s = -1.01 , -1.001 , -1.0001 , -1.00001  вычислить нормы матриц R.

В А Р И А Н Т     N 6

1. Построить процедуру вычисления матрицы по заданным векторам  x, y:

A =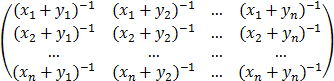

2. Для  x_k = 1/cos(k) , k=1, …, 5  и  y_k = k , k=1, …, 4  решить три системы уравнений  Az = b , где  y₅ = 1.01 , 1.001 , 1.0001 , а компоненты вектора  b  вычисляются по формуле  b_k = 2^k . Сравнить решения, полученные с двойной и стандартной точностями, используя программы  DECOMP  и  SOLVE.

В А Р И А Н Т     N 7

Составить процедуру формирования матриц  H  и  A  по формулам

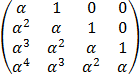H = ,     A = bE + H

Решить ряд линейных систем  Ax = b , где взять  a = 10 , b = 0.1 , 0.01 , 0.5 , 1.0  ;  b_k = tg(k) , используя программы  DECOMP  и  SOLVE. Сравнить решения, получаемые со стандартной и двойной точностью.

В А Р И А Н Т     N 8

Составить процедуру вычисления по заданной матрице  A(N,N)  матрицы  R = A^-1A - E  и ее нормы   .

Построить три матрицы  A  при x_k = (1+cos(k))/sin²(k) , k=1, …, 4 и 

x₅ = (1+cos(1))/sin²(1+e)  для трех значений  e = 0.001 , 0.00001 , 0.000001  и  N=5.

A =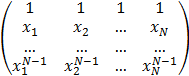

Исследовать зависимость погрешности вычисления    от e .

В А Р И А Н Т     N 9

1. Составить процедуру вычисления  матрицы  R  и ее нормы    по заданной матрице  A :  R = A^-1A - E ,

2. Построить несколько вариантов матрицы  A , зависящей от параметра d = 1.01 , 1.001 , 1.0001

A_ik  =    ,   N = 5 .

Вычисляя  A^-1  по процедурам  DECOMP  и  SOLVE , исследовать зависимость    от  d .

В А Р И А Н Т     N 10

Составить процедуру вычисления матрицы

A=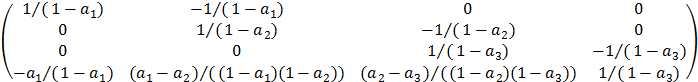

Решить ряд линейных систем  Ax=b , где  b_k = cos(k) , a₁ = 1.01 , a₂ = 1.001 , a₃ = var = 1.01 , 1.001 , 1.0001 , используя  DECOMP  и  SOLVE . Сравнить решения, полученные с обычной и двойной точностью.

В А Р И А Н Т     N 11

Составить процедуру вычисления матрицы

A =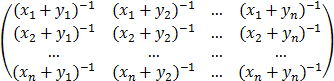

Полагая  y_k = cos(k) , k=1, …, 5 ;  x_k = 1/(1+k) , k = 1, …, 4  и задавая три варианта  x₅ = 0.9 , 0.99 , 0.999 , исследовать поведение матрицы  R = A^-1A - E  и ее нормы    от параметра  x₅ . Для вычисления  A^-1  использовать программы  DECOMP  и  SOLVE.

В А Р И А Н Т     N 12

Построить процедуру вычисления элементов матриц  H  и  A :

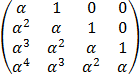H = ,     A = bE + H

Для  a = 2  и  b = 0.1 , 0.01 , 0.001  вычислить матрицу R = A^-1A - E  и ее норму   . Объяснить результаты.

В А Р И А Н Т     N 13

1.   Составить процедуру вычисления матрицы  A  вида

2.  

A =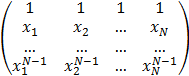

2. Используя ее, решить несколько раз линейную систему  Az=b , где  N=5,  b_k = 2^k + cos(k) , k = 1, …, 5 ;  x_k = k , k=1,…,4  и  x₅ = 1.1 , 1.01 , 1.001 , 1.0001 . Системы решать с обычной и двойной точностью, используя программы  DECOMP  и  SOLVE.  Сделать необходимые выводы.

В А Р И А Н Т     N 14