В А Р И А Н Т N 1
Для функции f(x) = 1/(1+25x2) по узлам xk = -1 + 0.1k (k=0,1,…20) построить полином Лагранжа L(x) 20-й степени и сплайн-функцию S(x). Затем сравнить значения трех интегралов:
; 
;
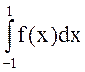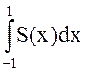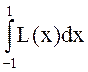. Первый интеграл вычислить аналитически, а для
вычисления последнего использовать программу QUANC8.
В А Р И А Н Т N 2
Для таблично заданной функции f(x)
|
x |
0.0 |
0.2 |
0.5 |
0.7 |
1.0 |
1.3 |
1.7 |
2.0 |
|
f(x) |
1.0 |
1.1487 |
1.4142 |
1.6245 |
2,0000 |
2.4623 |
3.2490 |
4.0000 |
построить сплайн-функцию и использовать ее для нахождения корня уравнения f(x) + 5x - 3 = 0 на промежутке [0 , 2] методом бисекции.
В А Р И А Н Т N 3
Для функции f(x) = 1/(1+25x2) по узлам xk = -1 + 0.1k (k=0,1,…20) построить полином Лагранжа L(x) 20-й степени и сплайн-функцию S(x). Вычислить значения всех трех функций в точках yk = -0.95 +0.1k (k=0,1,…19). Результаты отобразить графически.
Используя программу QUANC8, вычислить два интеграла:
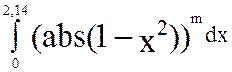, для m = -1 и для m =
-0.5.
В А Р И А Н Т N 4
Для
с шагом h=0.2
вычислить значения функции f(x) с использованием программы QUANC8, где 
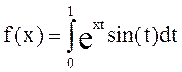. По полученным точкам построить сплайн-функцию и
полином Лагранжа 10-й степени. Сравнить значения сплайн-функции и полинома с
точным значением f(x) (вычислить интеграл аналитически) в точках xk=(k - 0.5) h для k=1,2,…10.
В А Р И А Н Т N 5
Для
с шагом
h=0.1 вычислить значения функции f(x) с
использованием программы QUANC8, где 
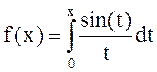. По полученным точкам построить сплайн-функцию и
полином Лагранжа 10-й степени. В точках
xk=(k - 0.5) h + 2 для k=1,2,…10 сравнить значения сплайн-функции и полинома с точным значением f(x) (вычислить интеграл по QUANC8 с высокой точностью).
В А Р И А Н Т N 6
По заданной таблице
|
x |
-1.000 |
-0.960 |
-0.860 |
-0.790 |
0.220 |
0.500 |
0.930 |
|
f(x) |
-1.000 |
-0.151 |
0.894 |
0.986 |
0.895 |
0.500 |
-0.306 |
построить полином Лагранжа и сплайн-функцию. Вычислить значения обеих функций в точках xk = -1 + 0.1k (k = 1,2,…,19). Построить графики.
Используя программу QUANC8, вычислить интеграл: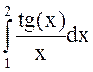 
.
В А Р И А Н Т N 7
Для функции f(x) = 1 - exp(-x) по узлам xk = 0.3k (k=0,1,…10) построить полином Лагранжа L(x) 10-й степени и сплайн-функцию S(x). Затем сравнить значения трех интегралов:
; 
;
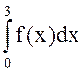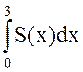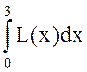. Первый интеграл вычислить аналитически, а для
вычисления последнего использовать программу QUANC8.
В А Р И А Н Т N 8
Для таблично заданной функции f(x)
|
x |
0 |
1.2 |
1.5 |
1.6 |
1.8 |
2.0 |
|
f(x) |
5.000 |
6.899 |
11.180 |
13.133 |
18.119 |
25.000 |
построить сплайн-функцию и использовать ее для нахождения корня уравнения
f(x) = 6x + 3 на промежутке [1 , 2] методом бисекции.
В А Р И А Н Т N 9
Для 
с
h = 0.1 вычислить значения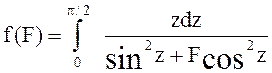 
, используя для вычисления интеграла программу QUANC8. По полученным точкам
построить сплайн-функцию и полином Лагранжа 10-й степени. Сравнить значения
обеих аппроксимаций в точках Fk = 0.55 + 0.1k (k=0,1,..,9).
В А Р И А Н Т N 10
Для
с шагом
h=0.2 вычислить значения функции f(x) с
использованием программы QUANC8, где 
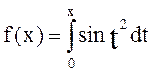. По полученным точкам построить сплайн-функцию и
полином Лагранжа 6-й степени. В точках
xk = 1.6 + 0.2k для k=0,1,…5 сравнить значения сплайн-функции и полинома с точным значением f(x) (вычислить интеграл по QUANC8 с высокой точностью).
В А Р И А Н Т N 11
Для функции f(x) = 1/(1+x) по узлам xk = 0.1k (k=0,1,…10) построить полином Лагранжа L(x) 10-й степени и сплайн-функцию S(x). Вычислить значения всех трех функций в точках yk = 0.05 +0.1k (k=0,1,…9). Результаты отобразить графически.
Используя программу QUANC8, вычислить два интеграла:
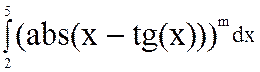, для m = -1 и для m =
-0.5.
В А Р И А Н Т N 12
Для функции f(x) = sin(x2) по узлам xk = 0.2k (k=0,1,…6) построить полином Лагранжа L(x) 6-й степени и сплайн-функцию S(x). Затем сравнить значения трех интегралов:
; 
;
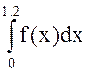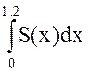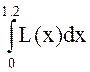. Для вычисления первого и последнего интегралов
использовать программу QUANC8.
В А Р И А Н Т N 13
Для таблично заданной функции f(x)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
