Процедура формирования матрицы. Норма вектора и матриц, страница 2

Разработать процедуру формирования матрицы  A(N,N)  с элементами  A_ik = min[ i , k ] . С помощью программ  DECOMP  и  SOLVE  обратить матрицу  A. Найти решение системы  Ax=b  по формуле  x = A^-1b  и найти нормы невязок: r(N) =   при  N = 4, 6, 10 , где   =  .  b_k = cos(k) . Проанализировать результаты.

В А Р И А Н Т     N 15

Матрица  P  зависит от параметра a и формируется следующим образом :

P_kk = a  ,  P_ik = 1  äëÿ  i¹k  . Разработать процедуру ее построения. Решить систему  Py = b , где  b = (1, 2, …, N)^T , используя программы DECOMP и SOLVE при  N=5  и  a = 0.99 , 1.0001 , 3.99 , 3.99999 . Сравнить решения со стандартной и двойной точностью.

В А Р И А Н Т     N 16

Написать процедуру формирования матрицы  B  по формулам:

B_ik =

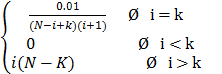
Вычислить матрицу  B^-1 , используя процедуры  DECOMP  и  SOLVE , и найти норму матрицы  R = BB^-1 - E  для  N = 3, 6, 9 . Îáúÿñíèòü ðåçóëüòàòû. 

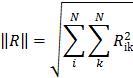
В А Р И А Н Т     N 17

Разработать процедуру формирования матрицы  Q

Q = 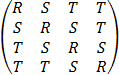, где  R = , S =

T = ,   Q - параметр.   Исследовать зависимость нормы матрицы  U=QQ^-1 - E  от параметра  Q = 0.01;  0.0001;  3.14;  3.18 .  

В А Р И А Н Т     N 18

Написать процедуру формирования матрицы  A  в зависимости от параметра  a . Ее ненулевые элементы задаются формулами:

A_ii = a^|N-2i|/2  ,  A_1k = A₁₁/a^k  (k¹N) ,   A_k1 = A_1k  (k¹N) ,   A_Nk = A_kN = A_NN/a^k

Вычислить матрицу  A^-1   и матрицу  R = E - A^-1A , а также норму матрицы  R  для  a = 1 ,  10 ,  100  и  N=4. Использовать программы  DECOMP  и  SOLVE.  Проанализировать результаты.   .

В А Р И А Н Т     N 19

Разработать процедуру формирования матрицы  B  по формулам 

B_ik = exp(ikh) , где  h - параметр. Решить систему  Bz = c ,  где  c = (1, 1, …, 1)^T  с помощью программ  DECOMP  и  SOLVE. Проанализировать результаты, полученные с обычной и двойной точностью для   h = 0.01;  0.0001; -10.0;  -100.0 и  N=5.

В А Р И А Н Т     N 20

Составить процедуру построения матрицы  C  по формулам :

C_ik =

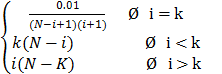
Сравнить между собой решение системы  Ax₁ = b , полученное с помощью  DECOMP  и  SOLVE,  с решением  x₂ = A^-1b , где  A^-1  также вычисляется с помощью этих программ. Найти относительную ошибку для  N=6 :

 , где   ,   а  b_k = k .

В А Р И А Н Т     N 21

Составить процедуру формирования матрицы  C  по формулам:

C_ik = d + log₂(ik) , где  d - параметр. Вычислить с помощью DECOMP и SOLVE матрицу  C^-1 , найти матрицу  R = E - C^-1C  и ее норму. Проанализировать решения при  N=5  и  d = 10;  1000;  10000 .  

В А Р И А Н Т     N 22

Написать процедуру вычисления симметрической матрицы  Q  и вектора  z  по заданным числам  a_k , b_k ,  g_k  ,  где

Q = 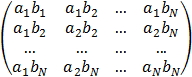 ,   z_i = b_i

Решить систему уравнений  Qx = z  с помощью  DECOMP  и  SOLVE , если  N=5,  a_k = k² ,  b_k = k + b ,  g_k = |k-3|  при следующих значениях параметра  b :  -0.9 ;  -1.1 ,  -1.19 ,  -1.199 .  Так как  g_k - компоненты вектора точного решения (убедиться в этом!), использовать  g  для оценки погрешности по формуле :   , где   .  Объяснить результаты.

В А Р И А Н Т     N 23

Написать процедуру вычисления матрицы  Q  и вектора  z  по заданным числам  a_k , b_k ,  g_k ,  a_k ,  где

Q = 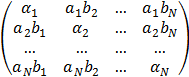 ,   z_i =

Решить систему уравнений  Qx = z  с помощью  DECOMP  и  SOLVE , если  N=5,  a_k = (N-k+1)² ,  b_k = 2^k-2 ,  g_k = 2^k ,  a_k = 2^k + g  при следующих значениях параметра  g :  1.0 ;  0.1 ,  0.01 .  Так как  g_k - компоненты вектора точного решения (убедиться в этом!), использовать  g  для оценки погрешности по формуле :   , где   .  Объяснить результаты.

В А Р И А Н Т     N 24

Написать процедуру вычисления матрицы  Q  и вектора  z  по заданным числам  N , x ,  y ,  a ,  g_k  где

Q = 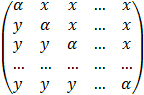 ,   z_i =

Решить систему уравнений  Qw = z  с помощью  DECOMP  и  SOLVE , если  N=6 ,  a = 4 ,  x = 4 + g,  y = 4 - g ,  g_k = 2^k-4  при следующих значениях параметра  g :  1.0 ;  0.5 ,  0.25 , 0.125.  Так как  g_k - компоненты вектора точного решения (убедиться в этом!), использовать  g  для оценки погрешности по формуле :   , где   .  Объяснить результаты.

В А Р И А Н Т     N 25

Написать процедуру вычисления матрицы  A  и вектора  z  по заданным числам  N ,  a ,  g_k  где

A = 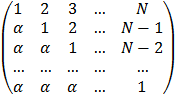 ,   z_i =

Решить систему уравнений  Ax = z  с помощью  DECOMP  и  SOLVE , если  N=6 ,  g_k = 2^k-2  при следующих значениях параметра  a :  0 ;  0.25 ,  0.49 , 0.499.  Так как  g_k - компоненты вектора точного решения (убедиться в этом!), использовать  g  для оценки погрешности по формуле :   , где   .  Объяснить результаты.