Коэффициент передачи объекта регулирования. Структурная схема системы автоматического управления и выбор регулятора, страница 2

По данным Таблицы 1, построен график «Линия равного запаса устойчивости», рис 2. По графику выбираем настройки регулятора, расположенные чуть правее экстремальной точки линии равного запаса устойчивости, которые обеспечивают минимум квадратичного интегрального критерия качества: 

и окончательно принимаем их равными k1=0,443 и k2=0,0126.

4. Построение переходного процесса по управляющему воздействию методом трапециидальных характеристик по ВЧХ замкнутой системы

Для построения ВЧХ замкнутой системы необходимо знать ее передаточную функцию по каналу управления, она выглядит так:

Подставив значения передаточных функций для каждого элемента,  заменив оператор Лапласа (p) на (jw), используя формулу Эйлера и избавившись от мнимости в знаменателе, после разделения получим мнимую и вещественную части в следующем виде:

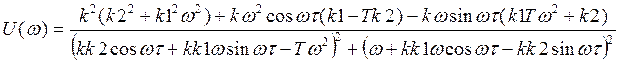
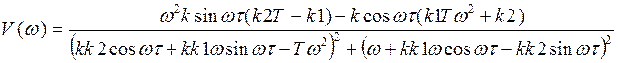
АЧХ  вычисляется по формуле:

Все эти величины определяем при изменении частоты w. Результаты этого расчета приведены в таблице 2.

Таблица 2

По данным первых двух столбцов построена ВЧХ замкнутой системы по управляющему воздействию, которая представлена на рисунке 3. По данным 1-го и 4-го столбцов построена АЧХ, изображенная на рисунке 4. Полученную кривую ВЧХ заменяем ломаной линией, в результате чего получаем ряд типовых трапеций. Трапециидальная характеристика определяется высотой r при частоте w=0, интервалом равномерного пропускания w_о, интервалом положительности w₁ и коэффициентом наклона х=w_о/w_1.  Все характеристики для каждой трапеции сведены в таблицу 3.

Таблица 3

Для каждой трапеции по таблицам приложения в литературе [1] определены значения h-функций при соответствующих коэффициентах наклона для наиболее оптимальных промежутков времени Dt. Для получения координат пригодных для построения кривой переходного процесса используют следующие зависимости