4. Малые колебания систем с распределенными параметрами
4.1 Предварительные замечания
При анализе колебаний систем с конечным числом степеней свободы модель системы считается состоящей из элементов двух видов
· инерционные элементы, представляющие собой абсолютно твердые тела,
· упругие элементы, лишенные массы (безинерционные).
Задача движения системы с конечным числом степеней свободы свелась к решению системы n обыкновенных дифференциальных уравнений (дифференцирование – по времени), где n – число степеней свободы, с некоторыми начальными условиями (t=0).
Все реальные объекты имеют массу и упругие связи, непрерывно распределенные по объему, т.е. состоят из бесконечного числа материальных точек. Такие системы называют системами с распределенными параметрами.
Пусть x, y, z - координаты точек тела в положении равновесия, тогда компоненты перемещения элементарных масс относительно положения представляют собой непрерывные функции координат и времени:
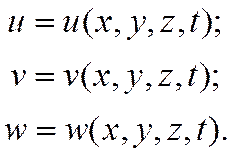
Уравнения статического равновесия систем с распределенными параметрами (стержней, плит и т.д.) представляют собой дифференциальные уравнения относительно перемещений, где дифференцирование ведется по координатам. Например,
уравнение равновесия стержня при изгибе:
![]()
уравнение равновесия изгиба пластины
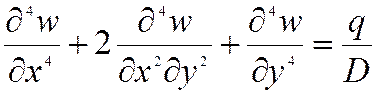
На основании принципа Даламбера уравнение вынужденных колебаний можно записать в форме уравнений статического равновесия, если дополнить внешние силы силами инерции и силами неупругого сопротивления.
Таким образом, на смену системе обыкновенных дифференциальных уравнений, описывающих систему с конечным числом степеней свободы, приходят
Краевая задача – уравнения + граничные условия.
4.2 Продольные колебания стержней.
4.1 Уравнение движения и граничные условия
Действие на стержень переменной во времени продольной нагрузки
![]() вызывает его продольные колебания.
Считаем при этом, что стержень достаточно тонкий и перемещением масс, связанным
с поперечной деформацией пренебрегаем.
вызывает его продольные колебания.
Считаем при этом, что стержень достаточно тонкий и перемещением масс, связанным
с поперечной деформацией пренебрегаем.
Напомним некоторые соотношения, известные из и полученные с их помощью уравнения статического равновесия
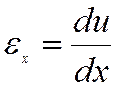 ;
;![]()
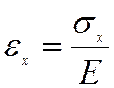 ;
;
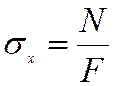 ;
; 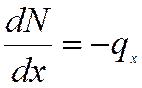 ;
;
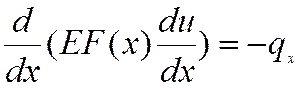 .
.
При действии на стержень переменной во времени продольной
нагрузки ![]() :
:
![]()
![]()
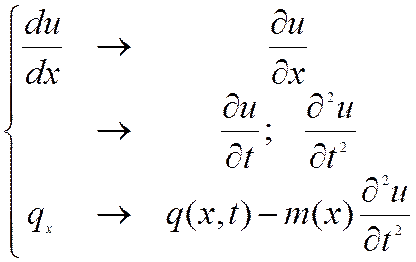
Здесь![]() - погонная масса стержня.
- погонная масса стержня.
Тогда уравнение движения без учета сил сопротивления имеет вид
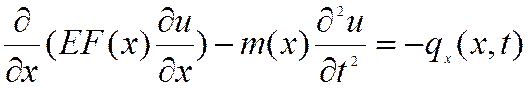 .
.
Граничные условия:
 |
![]()
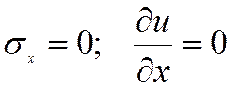
Геометрические граничные условия (перемещения) Динамические граничные условия (продольные силы)
Динамические граничные условия (продольные силы)
 Сила инерции и упругая сила,
приложенные к массе, находятся в равновесии:
Сила инерции и упругая сила,
приложенные к массе, находятся в равновесии:
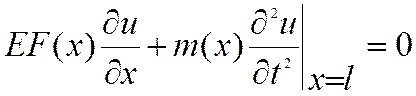 .
.
Динамические граничные условия (продольные силы)
 Две упругие силы
находятся в равновесии:
Две упругие силы
находятся в равновесии:
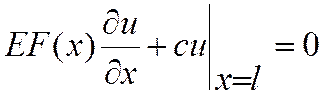
4.2 Свободные колебания
Рассмотрим случай ![]() и
и ![]() .
.
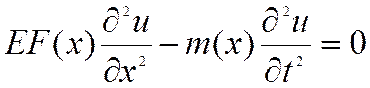 .
.
Полученное уравнение – уравнение малых колебаний – линейное, т.к. перемещения и их производные входят в первой степени. Ищем общее решение в виде суперпозиции частных. Используем метод разделения переменных, а именно, частное решение представляем в виде произведения двух функций, одна из которых зависит только от X, а вторая только от t
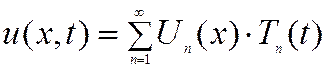 .
.
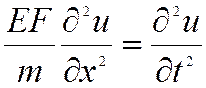 .
.
Обозначим 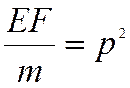 .
.
Тогда после подстановки частного решения получаем:
![]()
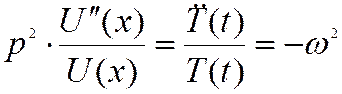 Так как левое
отношение не содержит t , а правое не содержит x, то ни одно из них не имеет переменных, а , следовательно,
является константой, которую обозначим …
Так как левое
отношение не содержит t , а правое не содержит x, то ни одно из них не имеет переменных, а , следовательно,
является константой, которую обозначим …
Тогда уравнение движения оказывается эквивалентным двум уравнениям в обычных производных
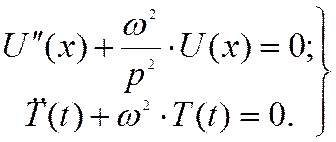
Частное решение для функции U(х):
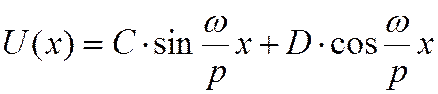 , где постоянные С и D определяются из граничных условий.
, где постоянные С и D определяются из граничных условий.
Частное решение для функции T(t):
![]() , где амплитуда и фаза
определяются начальными условиями.
, где амплитуда и фаза
определяются начальными условиями.
А что же ![]() Для определения
этого параметра как и раньше – процедура отыскания ненулевого решения. Покажем
на примере.
Для определения
этого параметра как и раньше – процедура отыскания ненулевого решения. Покажем
на примере.
 |
![]()
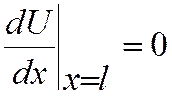
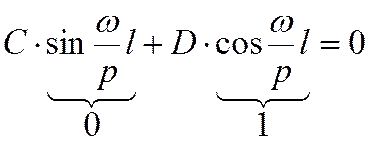
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.