В1 «Устойчивость» – термин перегруженный по частоте его использования. Устойчивость: движения; равновесного состояния; процесса (например, вычислений); отношений между людьми и др.
Что же понимается под устойчивостью? В поисках ответа на этот вопрос мы сталкиваемся с перегруженностью уже формулировки строгого математического определения. Дадим нестрогое определение, сформулировав его для механической системы.
Состояние движения (или его частного случая – равновесия) механической системы устойчиво, если малые возмущения приводят к малым отклонениям от этого состояния, и неустойчиво, если малым возмущениям отвечают большие отклонения.
Под возмущением понимаются некоторые изменения обобщенных координат и (или) скоростей, вызванные внешней по отношению к рассматриваемому процессу причиной.
Хорошо знакомы иллюстрации понятия устойчивости:
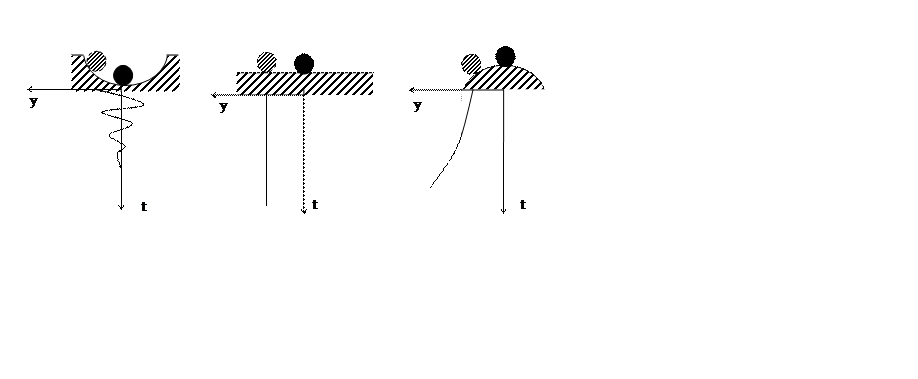
Дополним их еще двумя ситуациями,

в которых поведение шарика при смещениях, ограниченных размерами впадины,
свидетельствует об устойчивости этого положения. Если же допустить бŏльшие
перемещения, то положение шарика следует признать неустойчивым. В таком случае
говорят , что система устойчива в малом и неустойчива в большом.
Понятно, что приведенное определение следовало бы дополнить описанием понятий
«большое» и «малое», мы ограничимся лишь указанием на это.
Сокращая представление о механических системах до интересующих инженера-строителя моделей сооружений и конструкций, бŏльшую часть курса посвятим устойчивости равновесия. В качестве задачи об устойчивости движения будет рассмотрена примеры флаттер и шимми.
Говоря об устойчивости равновесных состояний, проблему разделяют на
Примерами нарушения устойчивости положения являются опрокидывание крана или сдвиг подпорной стенки, происходящие в результате нарушения равновесия внешних сил, действующих на сооружение.
Проблема устойчивости формы равновесия деформируемых систем представлена ситуациями, когда система теряет первоначальную форму равновесия, соответствующую приложенной нагрузке, и вынужденно приобретает другую или вовсе приходит в движение.
В строительном деле потеря устойчивости рассматривается как исчерпание работоспособности конструкции (потеря устойчивости верхнего пояса фермы).
Корабелы и авиаконструкторы допускают потерю устойчивости некоторых элементов в упругой стадии (обшивка палуб, пластины между ланжеронами во время полета.)
Основной тип графика – диаграмма равновесных состояний – зависимость между величиной приложенной к системе нагрузки и характерным отклонением.
Призматический стержень, одна из опор которого может перемещаться вдоль оси стержня. При воздействии на такую систему сжимающей силы, линия действия которой совпадает с осью стержня по мере роста силы можно отметить три характерные ситуации в зависимости от силы Р:

|
Р<Pк |
P=Pк |
P>Pк |
|
Первоначальная форма равновесия – прямолинейная – устойчива |
Точка бифуркации – разветвления |
Три возможных положения равновесия, среди которых первоначальное - неустойчиво |
Отметить смежность форм устойчивого равновесия.
Два жестких стержня соединены шарниром, левая опора – шарнирно неподвижная, правая жестко препятствует вертикальному перемещению и упруго препятствует горизонтальному перемещению.
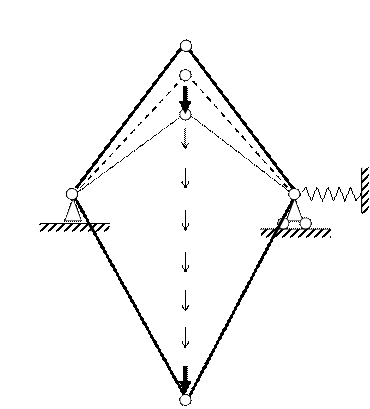 Диаграмма равновесных состояний
имеет вид:
Диаграмма равновесных состояний
имеет вид:

По мере роста силы последовательно возникают характерные состояния мембраны:
|
Р<Pк |
P=Pк |
P>Pк |
|
|
При возрастании силы |
Увеличивается вертикальное перемещение узла, уменьшается стрела. Возмущения, не приводящие к нарушению условия Р<Pк исчезают после снятия причин – положение равновесия устойчиво. Уменьшается жесткость системы |
Мгновенное перемещение узла на конечное расстояние - прощелкивание |
Сила не сжимает , а растягивает стержни. Положение равновесия устойчиво. |
При снятии нагрузки система займет положение, соответствующее зеркальному отражению первоначального. Чтобы вернуть систему в исходное состояние, нужно приложить силу противоположного направления, Когда ее значение достигнет критического, произойдет обратный перескок.
Отрезок, обозначенный пунктирной линией, не соответствует реально осуществляемым положениям равновесия.
Первоначальная форма соседствует с неустойчивой формой равновесия, а устойчивая находится на отдалении.
Примеры: мембраны, масленка, цилиндрические оболочки.
 Пример: брансбойт, реактивные
силы.
Пример: брансбойт, реактивные
силы.
Комментарий к диаграмме равновесных состояний следующий:
Следящая сила неконсервативна:

![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.