II семестр ЛЕКЦИЯ 7
· Ранее рассмотрены формы равновесия симметричной фермы Мизеса
4.8 Критерий устойчивости равновесия Лагранжа
Если касательная жесткость системы в данном положении равновесия положительна, то положение равновесия устойчиво.
Согласно этому утверждению точки на восходящих участках кривой симметричных равновесных состояний фермы отображают устойчивые, а точки нисходящего участка 1-3 – неустойчивые состояния равновесия.
Для системы с n
степенями свободы ( в нашем случае n=2 при несимметричной деформации фермы Мизеса) критерий
устойчивости Лагранжа связывает оценку устойчивости со знаком определителя касательной
матрицы жесткости: ![]() . Иными словами, если для
найденного положения равновесия касательная матрица жесткости является
положительно определенной, то это положение равновесия устойчиво.
. Иными словами, если для
найденного положения равновесия касательная матрица жесткости является
положительно определенной, то это положение равновесия устойчиво.
4.9 Нелинейные колебания фермы Мизеса
Считаем, что центральный узел несет на себе сосредоточенную массу.
Уравнения движения системы с двумя степенями свободы
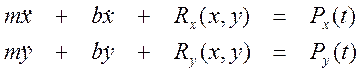
В случае больших перемещений (например, свободные колебания при большом начальном отклонении) упругие восстанавливающие силы являются функциями положения узла.
В матричном виде при отсутствии вязкости:
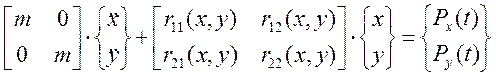
или
![]() .
.
В отличие от линейной задачи матрица ![]() зависит
от положения узла.
зависит
от положения узла.
В случае свободных колебаний 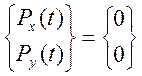 .
.
Напоминание:
Линейная задача: ![]() ;
;
Решение задачи о линейных свободных колебаниях
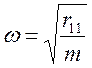 ;
;В случае нелинейных колебаний такого решения для свободных колебаний нет.
Переменная жесткость → неприменимы понятия собственная частота и амплитуда:
Фазовая диаграмма – еще один вид графика, используемый при исследовании движения – зависимость между положением точки и ее скоростью.
В случае малых колебаний относительно положения равновесия
фазовая диаграмма представляет собой замкнутую кривую при ![]() (кривая 1) и спираль вокруг точки
устойчивого равновесия при
(кривая 1) и спираль вокруг точки
устойчивого равновесия при ![]() .
.
При больших отклонениях колебания несимметричны: смещение внутрь больше смещения во вне (кривая 2).
При значительных отклонениях траектория массы охватывает
верхнее и нижнее положения равновесия, а в случае наличия диссипации (![]() ) совершает затухающие колебания
относительно одного их этих положений.
) совершает затухающие колебания
относительно одного их этих положений.

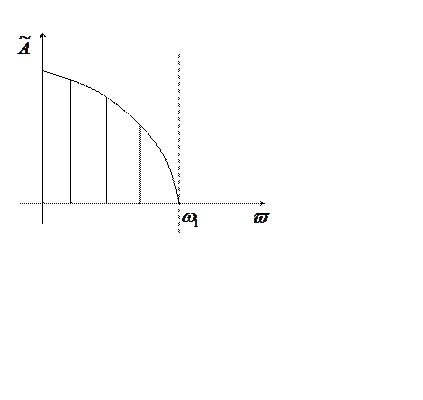
Условная частота свободных колебаний зависит от начального возмущения.
Скелетная кривая → зависимость условной частоты от условной амплитуды. Вид кривой зависит от характеристики жесткости системы.
4.10 Оценка устойчивости равновесия на основании анализа движения
А. Формы равновесия симметричной фермы Мизеса при отсутствии нагрузки.
Для рассматриваемой системы можно указать пять равновесных форм (см. рис.): переведя центральный узел в любое из указанных положений, мы отметим отсутствие движения.
Устойчивость положений равновесия проверим, задавая малые отклонения от него или (и) придавая малую начальную скорость.
Если система находится в положении 1 или в положении 2, то такие возмущения повлекут за собой малые колебания, при наличии диссипации – затухающие, относительно исследуемого положения равновесия. Такое поведение системы свидетельствует об устойчивости данного положения равновесия по отношению к выбранному возмущению.
Остальные равновесные состояния следует признать неустойчивыми, т.к. их малые возмущения приведут к движению и затем к колебаниям относительно одного из устойчивых положений равновесия 1 или 2.
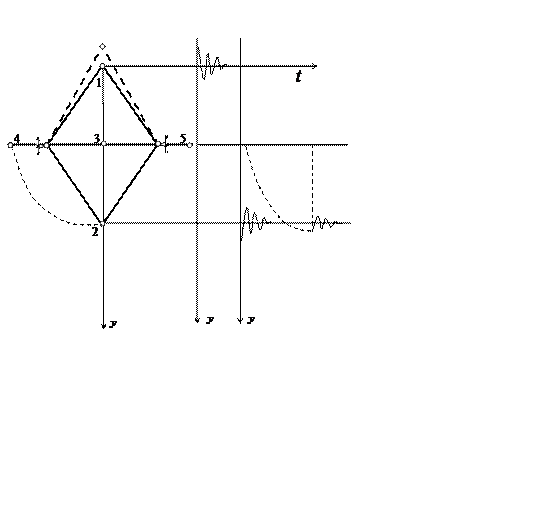
Б. Определение критической силы.
Рассматриваем нагружение системы вертикальной силой в центральном узле. Пусть сила вырастает с некоторым шагом от 0 до максимального значения Рmax за время Т.
Считаем нагрузку медленно возрастающей, т.е. считаем, что силы инерции появляются только при движении, вызванном потерей устойчивости.
Уравнения статики
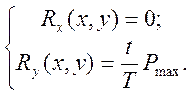
Условия для отыскания критической силы
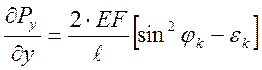 - при сохранении
симметричной формы равновесия;
- при сохранении
симметричной формы равновесия;
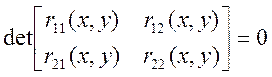 - при приобретении смежной
формы равновесия.
- при приобретении смежной
формы равновесия.
Следует произвести расчеты для некоторой последовательности значений Ро, следя за графиком у(t) и фазовой диаграммой.
Первая форма движения при потере устойчивости



Вторая форма движения при потере устойчивости
Исследуем устойчивость движения по отношению к горизонтальному возмущению.
Для этого произведем те же действия, что и в первом случае, но при некотором начальном горизонтальном смещении. Центральный узел при росте силы опускается вниз, совершая покачивания поперек основного движения.
Для низких ферм процесс оказывается устойчивым по отношению к поперечному возмущению, существенного изменения критической силы не получим.
При высоте фермы больше 1.2 пролета произойдет резкий выход центрального узла в сторону и скачкообразный переход к конечному устойчивому состоянию через боковое.
Т.е происходит потеря устойчивости основного движения.
В критической точке становятся возможными две формы равновесия – симметричная неустойчивая и смежная боковая устойчивая. Точка бифуркации.
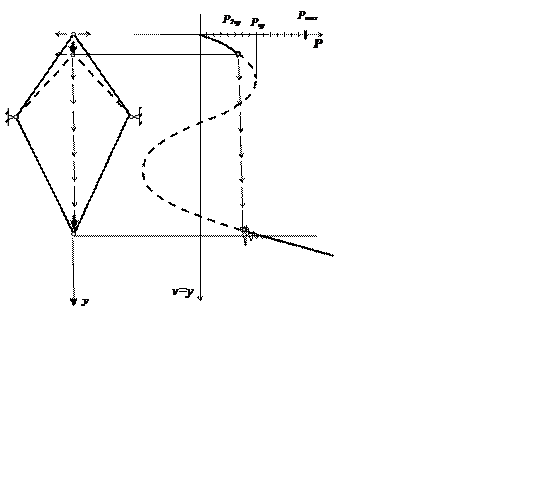
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.