4.3 Изгибные колебания балок.
4.3.1 Уравнение движения и граничные условия
При исследовании попреречных колебаний стержня воспользуемся всеми допущениями, предписываемыми технической теорией изгиба:
Тогда, дифференциальное уравнение изогнутой оси для случая равновесия балки имеет вид
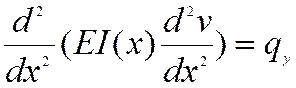 .
.
При действии на стержень переменной во времени поперечной
нагрузки 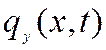 :
:
![]()
![]()

Здесь![]() - погонная масса стержня.
- погонная масса стержня.
Полученное для случая равновесия стержняможно применить к случаю движения , воспользовавшись принципом Даламбера, т.е. добавляя к распределенной нагрузке погонные силы инерции, интенсивность которых определится произведением погонной массы на ускорение. Тогда без учета сил сопротивления уравнение движения имеет вид
(1) 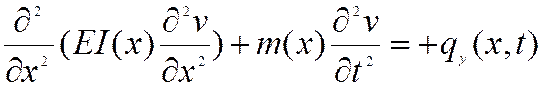 .
.
Это есть линейное уравнение четвертого порядка в частных производных. Его решение – функция прогибов в интервале изменения x от 0 доl, содержащая 4 постоянные интегрирования.
Постоянные интегрирования определяются поведением функции прогибов по торцам, т.е. условиями закрепления концевых сечений.
(2) Граничные условия:
 |
|
|
|
|
|
|
Геометрические граничные условия (перемещения) – включают в себя перемещения и углы поворота. Динамические граничные условия – те, которые содержат поперечные силы и моменты, т.е. –производные ботлее высоких порядков.
 |
|
|
|
|
|
|
(3) Условия начала движения.
4.3.2 Свободные колебания

.
Полученное уравнение – уравнение малых колебаний – линейное, т.к. перемещения и их производные входят в первой степени. Ищем общее решение в виде суперпозиции частных. Применим к нему метод разделения переменных, а именно, частное решение представляем в виде произведения двух функций, одна из которых зависит только от X, а вторая только от t
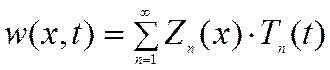 .
.
Тогда после подстановки частного решения получаем: ![]()
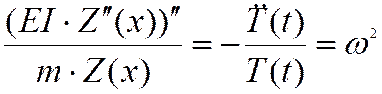 Так как левое
отношение не содержит t , а правое не содержит x, то это равенство возможно только в том случае, если каждая
из функций постоянна. Обозначим ее
Так как левое
отношение не содержит t , а правое не содержит x, то это равенство возможно только в том случае, если каждая
из функций постоянна. Обозначим ее ![]() .
.
Тогда уравнение движения оказывается эквивалентным двум уравнениям в обычных производных

Частное решение для функции T(t):
![]() , где амплитуда и фаза
определяются начальными условиями.
, где амплитуда и фаза
определяются начальными условиями.
Это уравнение показывает, что ![]() есть
частота свободных колебаний балки.
есть
частота свободных колебаний балки.
↓
При определении констант первого из уравнений сталкиваемся опять с процедурой отыскания ненулевого решения однородной системы уравнений:
↓
Интегрируя первое уравнение и составляя граничные условия для определения констант , мы убеждаемся, что ненулевое решение имеет место тогда, когда принимает определенные значения, являющиеся собственными частотами балки.
Собственные частоты нумеруем в порядке возрастания.
↓
Каждому значению собственной частоты ![]() соответствует собственная форма
колебаний
соответствует собственная форма
колебаний ![]() , удовлетворяющая первому из
уравнений. Конечно форма определена с точностью до постоянного множителя.
, удовлетворяющая первому из
уравнений. Конечно форма определена с точностью до постоянного множителя.
↓
Ортогональность собственных
форм: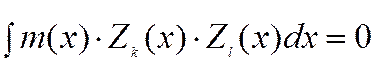 при
при ![]() .
.
↓
Вынужденные колебания – разложение по собственным формам.
4.3.3 Колебания балок постоянного сечения
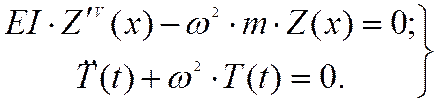
Для сокращения записи обозначим 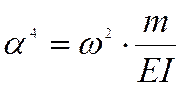 .
Тогда первое уравнение приобретает вид
.
Тогда первое уравнение приобретает вид
![]() .
.
Общий интеграл этого уравнения имеет вид
![]() .
.
Далее решается задача определения постоянных интегрирования из граничных условий.
Прежде, чем это проделать рассмотрим иную форму записи общего решения, имеющую значительные преимущества при организации вычислительного процесса, а именно представление общего интеграла с помощью функций А.Н. Крылова.
Известно, что линейная комбинация частных решений является также частным решением. В таком случае вместо гиперболических и тригонометрических синусов и косинусов используем в качестве частных решений следующие их линейные комбинации:
 ;
;
 ;
;
 ;
;
 .
.
Легко убедиться в следующих свойствах функций А.Н. Крылова:
·
Производная по Х каждой следущей функции ![]() равна
предыдущей
равна
предыдущей ![]() .
.
·
При х=0 ![]() .
.
Эти свойства позволяют назвать систему функций Крылова системой с единичной матрицей или частными решениями с единичной матрицей начальных значений.
Итак, общее решение уравнения для определения собственных форм колебаний записываем следующим образом:
 .
.
Примеры:
4.3.4 Балка, лежащая на двух опорах.
На каждой опоре равны нулю прогиб и изгибающий момент:
![]()

![]()

![]()
![]()
![]()
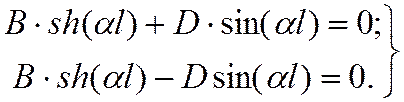
Далее повторяем рассуждения, связанные с решением однородной системы уравнений:
Условием получения ненулевого решения является равенство нулю определителя, а именно
![]()
![]() .
.
Это равенство эквивалентно двум следующим
![]() или
или ![]() . Первый вариант исключается, т.к.
гиперболический синус имеет ноль только в начале координат. Остается второй
вариант и, следовательно:
. Первый вариант исключается, т.к.
гиперболический синус имеет ноль только в начале координат. Остается второй
вариант и, следовательно:
![]() или
или
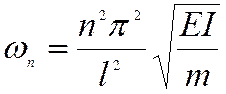
Заметим, что собственные частоты растут пропорционально квадрату номера, а не первой степени, как это было при продольных колебаниях.
После подстановки значения частоты из найденного ряда в однородную систему уравнений следует
![]()
Таким образом, только постоянная D оказалась отличной от нуля и частное решение уравнения свободных колебаний балки постоянного сечения имеет вид
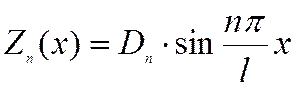 .
.
Значение ![]() выбирается из
соображений удобства вычислений – так называемая процедура нормирования.
Например, может быть использовано условие равенста 1 амплитуды формы, что
приводит к
выбирается из
соображений удобства вычислений – так называемая процедура нормирования.
Например, может быть использовано условие равенста 1 амплитуды формы, что
приводит к ![]() .
.
4.3.5 Консольно защемленная балка.
На каждой опоре равны нулю прогиб и изгибающий момент:
![]()
![]()

![]()
![]() ( при
дифференцировании функция V2 переходит в V1)
( при
дифференцировании функция V2 переходит в V1)
Далее повторяем рассуждения, связанные с решением однородной системы уравнений:
Условием получения ненулевого решения является равенство нулю определителя, а именно
![]()
![]() .
.
Отсюда ![]() .
.
Три первых корня этого уравнения 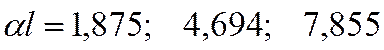
 |
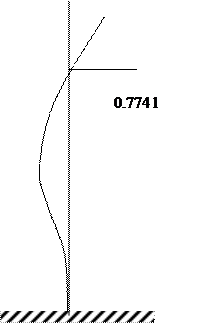 |
 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.