I семестр ЛЕКЦИЯ 3
1.7 Вынужденные колебания системы с одной степенью свободы
 |
|
· Гармоническая возмущающая сила · Внезапно приложенная сила · Импульс · ……..и т.д. |
1.7.1 Гармоническая возмущающая сила (вибрационная нагрузка)
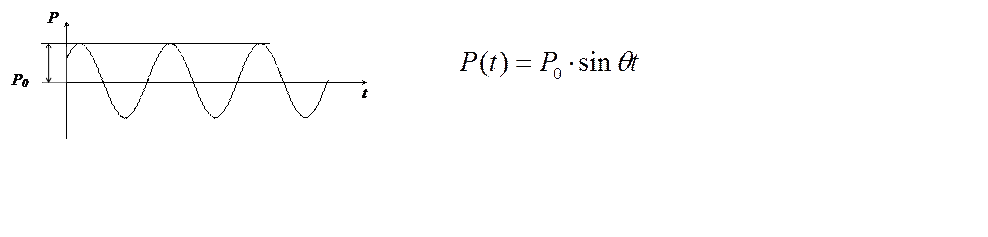
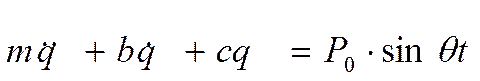
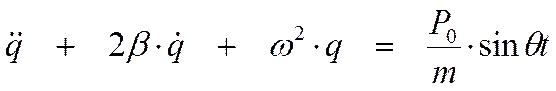
Общее решение дифференциального уравнения есть сумма общего решения однородного уравнения, т.е. уравнения, описывающего свободные колебания, и частного решения неоднородного уравнения
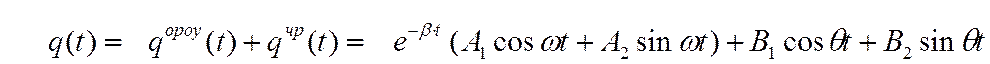 .
.
а) Сначала получим частное решение, которое
обеспечивает ненулевую правую часть. Для этого подставим выражение ![]() в уравнение . Опустим
подробности, но проанализируем этапы этого процесса: функции
в уравнение . Опустим
подробности, но проанализируем этапы этого процесса: функции ![]() и
и ![]() при
дифференцировании поочередно превращаются друг в друга, меняя периодически
знаки и приобретая коэффициенты. Поэтому в левой части уравнения окажется
некоторое выражение содержащее коэффициенты В1 и В2,
которые нужно найти, и функции
при
дифференцировании поочередно превращаются друг в друга, меняя периодически
знаки и приобретая коэффициенты. Поэтому в левой части уравнения окажется
некоторое выражение содержащее коэффициенты В1 и В2,
которые нужно найти, и функции ![]() и
и ![]() , а в правой части сохранится функция
, а в правой части сохранится функция
![]() с коэффициентом:
с коэффициентом:
.
Соединив все в левой части, получим сумму
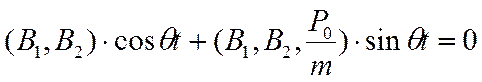 .
.
Здесь скобками обозначены коэффициенты при ![]() и
и ![]() ,
а внутри скобок показаны параметры, которые входят в соответствующие
алгебраические выражения. Так как это уравнение должно удовлетворяться при
любых значениях параметра t ,
и
,
а внутри скобок показаны параметры, которые входят в соответствующие
алгебраические выражения. Так как это уравнение должно удовлетворяться при
любых значениях параметра t ,
и ![]() и
и ![]() не
получают одновременно нулевые значения, то полученное уравнение эквивалентно
двум алгебраическим уравнениям относительно В1 и В2:
не
получают одновременно нулевые значения, то полученное уравнение эквивалентно
двум алгебраическим уравнениям относительно В1 и В2:
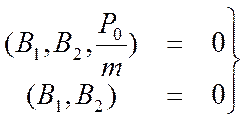 .
.
Решением этих уравнений являются следующие выражения коэффициентов
при ![]() и
и ![]() в
частном решении:
в
частном решении:
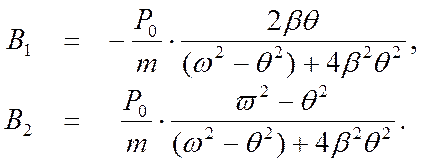
б) Теперь следует найти постоянные А1 и А2 частного решения однородного уравнения из начальных условий движения
![]() и
и 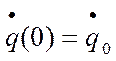 .
.
Итак ![]() :
:
![]()
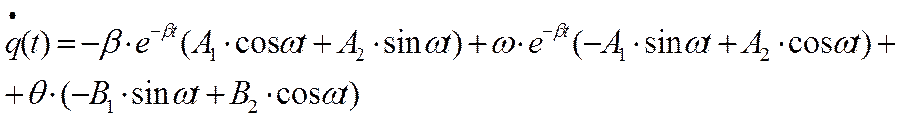
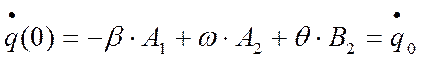
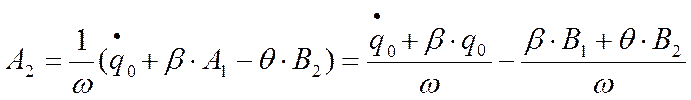 .
.
в) Запишем окончательный вид решения, сгруппировав частное решение в два выражения: одно из которых содержит начальные значения смещения и скорости, а второе – коэффициенты В1 и В2:
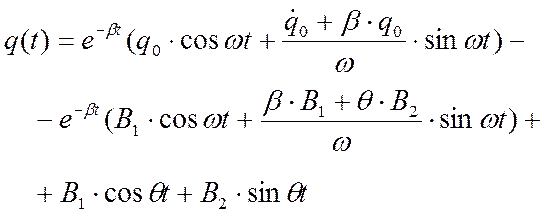
Таким образом, смещение при действии гармонического возмущения складывается из трех составляющих:
-
свободные затухающие колебания с частотой ![]() , зависящие от начальных условий;
, зависящие от начальных условий;
-
свободные затухающие колебания с частотой ![]() , независящие от начальных условий;
, независящие от начальных условий;
-
чисто вынужденные колебания с частотой ![]() .
.
Графики движения:

![]()
![]()
IV Установившиеся вынужденные колебания при вибрационной нагрузке описываются выражениями
![]()
или (с учетом того, что В1<0)
![]() (*)
(*)
Здесь
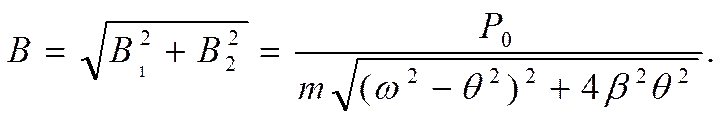
Для консервативной системы ( без потерь энергии)
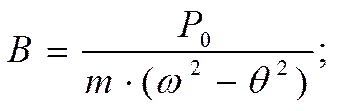
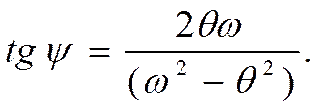 (**)
(**)
V Выводы:
Из (*): перемещения системы происходят с частотой возмущающей силы, но отстают по фазе.
Из (**):
-
при малых частотах возмущения ![]() по
сравнению с собственной частотой
по
сравнению с собственной частотой ![]() отставание
невелико;
отставание
невелико;
-
при равенстве частот возмущения и собственной ![]() , т.е. в тот момент, когда сила
максимальна, перемещение равно нулю.
, т.е. в тот момент, когда сила
максимальна, перемещение равно нулю.
VI Динамический коэффициент
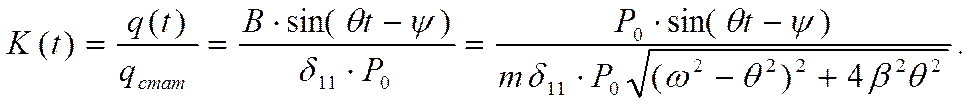

VII Амплитудно-частотная характеристика.

Выводы:
0сновной: Возникновение больших перемещений и, соответственно, и больших усилий и напряжений может происходить при малой величине возмущающей силы (в десятки раз меньшей, чем сила, опасная при статическом воздействии) за счет сближения частоты возмущающей силы и собственной частоты системы.
1 Учет сил вязкого сопротивления заметно влияет на величину коэффициента динамичности лишь в околорезонансной зоне и, следовательно,
- в удалении от резонанса можно использовать значения Кдин , полученные без учета вязкого сопротивления;
- во всей околорезонансной зоне можно принимать Кдин= Крезонанс.
2 Полученное решение показывает в случае консервативной системы неограниченный рост перемещений при совпадении частоты возмущения с собственной частотой, т.е. при резонансе. На самом деле этого не происходит, что объясняется тем, что само линейное уравнение правомочно лишь при малых перемещениях, при значительных перемещениях движение описывается нелинейным уравнением.
3 При наличии вязкого сопротивления
- увеличение коэффициента вязкого сопротивления приводит к уменьшению динамического коэффициента;
- перемещение не стремится к 0 при резонансе;
- смещение резонанса в сторону
4 В зарезонансной зоне
- уменьшение величины динамического коэффициента и приближение к оси абсцисс: перемещения оказываются меньше, чем статические;
- перемещения незначительны, но опасны для человеческого организма.
5 Стремление избежать возникновения резонанса имеет следующие пути реализации
- увеличение собственной частоты за счет изменения массы и жесткости;
- если это невозможно, то в процессе пуска и выключения обязательны специальные меры при прохождении через резонанс.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.