Разработка и исследование линейных непрерыных систем с модальными регуляторами, страница 4

ku=1/(C*inv(-Az)*B)

ku =

      151.9969

Проделанные вычисления позволяют реализовать моделирование процессов в среде Simulink.

2.2. Подготовка S–модели в среде Simulink.

На рис. 1 представлена блок-схема моделируемой системы.

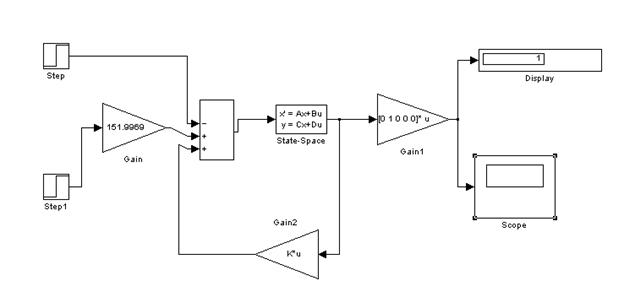
рис. 1

2.3. Исследование линейной непрерывной системы с модальным регулятором

2.3.1. Отработка ненулевых начальных условий.

В данном пункте требуется подобрать для вектора  такое значение, чтобы оно соответствовало постоянной величине выходной переменной . Поэтому: чтобы получить  нужно сделать . Пусть . Прочие переменные состояния могут быть любыми, поэтому есть смысл оставить их нулевыми. В итоге получаем график процесса, представленного на рисунке 2.

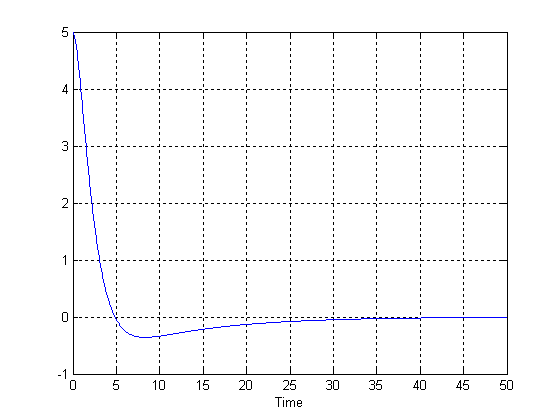
рис. 2

2.3.2. Ступенчатое изменение уставки.

В этом случае начальные условия и возмущение равны нулю. Уставка, вначале тоже равна 0. Так как входной сигнал постоянен, выходной стабилизируется к 1. В итоге получаем график процесса, представленного на рисунке 3.

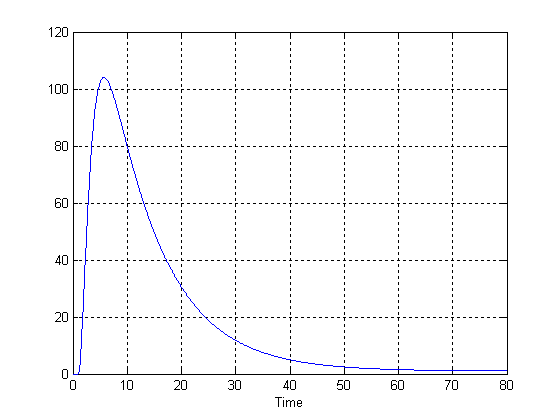
рис. 3

2.3.3. Ступенчатое изменение нагрузки.

В этом процессе уставка и начальные условия равны нулю. Система реагирует только на изменение нагрузки. В итоге получается график процесса, представленного на рисунке 4.

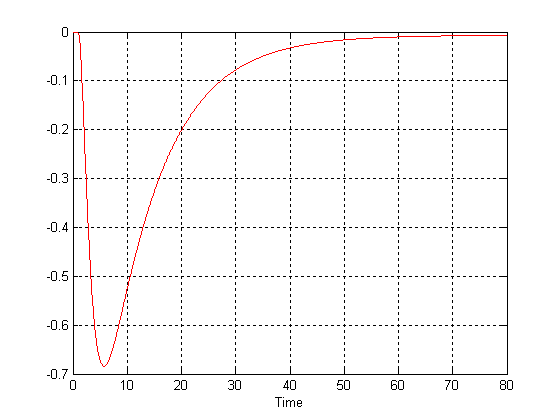
рис. 4

2.4. Сопоставление полученных результатов с моделью, построенной в среде Matlab.

Для проверки результатов работы Simulink в среде необходимо использовать функции step и initial.

2.4.1. Отработка ненулевых начальных условий.

Для моделирования этого процесса существует специальная функция initial, в нее подставляется сама модель с матрицей  замкнутой системы и вектор начального состояния.