Содержательное описание АСР. Описание функциональной схемы. Обоснование способа описания АСР напряжения сварочной дуги, страница 7

Для определения устойчивости системы по критерию Найквиста можно воспользоваться, так же, логарифмическими характеристиками разомкнутой системы, изображенными на рисунке 14. Для того чтобы замкнутая система была устойчива требуется, чтобы ЛФЧХ пересекала ось –180 градусов, правее точки пересечения ЛАЧХ оси 0 дб. Это условие выполняется.

Используя критерий Найквиста, по логарифмическим-частотным характеристикам можно легко определить запасы устойчивости.

Запас по фазе:

                           (6.14)

Запас по модулю:

           (6.15)

Воспользовавшись графиком определим: γ=33.5⁰, h=27 дб.

6.3. Исследование качества

6.3.1. Исследование точности в установившемся режиме

Значения составляющих ошибки в установившемся режиме можно определить с помощью теоремы о конечном значении:

                       (6.16)

где X_g=W_xG и X_f=W_xfF – изображения составляющих ошибки; G и F – изображения соответственно g и f – сигнал задания и возмущающие воздействия.

Анализируя структурную схему АСР (рисунок 3) можно выделить передаточную функцию регулятора с астатизмом первого порядка:

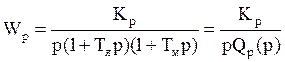             (6.17)

и статическую передаточную функцию объекта:

                                      (6.18)

На объект управления действуют два основных возмущения: напряжение сети и скорость подачи электрода – f₁ и f₂. По формулам (6.16) находим:

(6.19)

Система астатическая относительно задающего воздействия и относительно возмущений, таким образом, при постоянном задании и возмущениях ошибка в установившемся режиме отсутствует.

6.3.2. Исследование качества переходного процесса

6.3.2.1. Исследование по вещественной частотной характеристике

Определим вещественную частотную характеристику (ВЧХ) замкнутой системы P(w), для заданных значений:

(6.22)

График ВЧХ приведен на рисунке 17.

Рисунок 17. ВЧХ системы

Анализируя ВЧХ можно отметить, что ошибка в установившемся режиме равна нулю: P(0)=h(∞). ВЧХ не терпит разрыва, и, следовательно, система является устойчивой.

ВЧХ имеет выброс: P_max=1.85, определим величину перерегулирования:

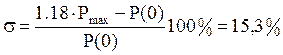                        (6.23)

Приблизительно определим время переходного процесса:

                                              (6.24)

6.3.2.2. Квадратичная интегральная оценка

Квадратичная интегральная оценка определяется следующим образом:

                      (6.25)

Значение функции рассогласования ε(t) определим выполнив обратное преобразование Лапласа над произведением единичного входного сигнала 1/р и передаточной функции замкнутой системы по ошибке (6.4).Подставив конкретные числовые значения получим:

(6.26)

Вычислив интеграл (6.25) получим значение квадратичной интегральной оценки для рассматриваемой системы:

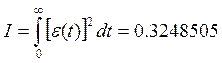    (6.27)

Заключение

В процессе выполнения контрольно-курсовой работы было продолжено изучение АСР сварочной дуги, начатое при разработке курсового проекта по курсу «Моделирование систем управления». Были исследованы передаточные функции элементов системы, а также передаточные функции разомкнутой системы от задающего возмущающего воздействия, изучены типовые динамические звенья которыми были представлены передаточные функции. Составлены выражения для весовых и переходных функций элементов разомкнутой системы и построены соответствующие графики. Найдены выражения для весовых и переходных функций разомкнутой системы от задающего и возмущающего воздействия к выходу. Построены частотный годограф, логарифмические частотные характеристики (ЛАЧХ и ЛФЧХ) отдельных функциональных элементов и всей разомкнутой системы в целом.

Было проведено исследование замкнутой системы и ее анализ. Определены основные передаточные функции замкнутой системы, главный оператор системы, передаточная функция замкнутой системы от возмущения к выходу. Исследована устойчивость замкнутой системы прямыми и косвенными методами.

 СПИСОК  ЛИТЕРАТУРЫ

1.  Бесекерский В.А., Попов Е.П. Теория систем автоматического      регулирования. М., Наука, 1975, 767 с.

2.  Макаров И.М., Менский Б.М. Линейные автоматические системы. М., Машиностроение, 1977, 464 с.

3.  Фомичев А.А. Теория автоматического управления. Методические указания по выполнению курсовых работ. Часть 1. Тула, ТулГУ, 2000, 82 с.