В пунктах 2 – 4 данной работы была построена и рассматривалась модель АСР напряжения сварочной дуги вида «вход – выход». Один из основных недостатков таких моделей заключается в том, что при использовании их для целей управления с помощью ЭВМ требуется запоминать все прошлые значения управляющего сигнала. Поэтому модели «вход – состояние - выход» (ВСВ), в которых состояние по определению является хранилищем всего прошлого поведения динамической системы, наиболее адекватны современным управляющим средствам.
Модели ВСВ представляют в векторно-матричной форме записи:
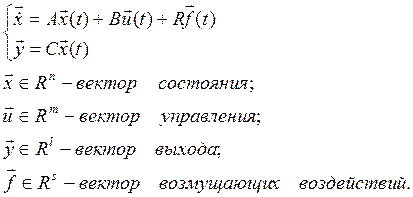(5.1)
Первое уравнение записанной системы – так называемое уравнение состояния, или уравнение «вход - состояние», здесь:
(5.2)
Так как модели ВСВ несут полную информацию о системе, то переход от них к моделям в терминах передаточных функций осуществляется однозначно, в тоже время одну модель типа «вход – выход» можно представить различными моделями ВСВ. Более того, для системы можно составить бесконечное число моделей типа ВСВ.
Из этого
множества выделяют так называемые модели в канонической форме. Переход к
канонической форме можно осуществить следующим образом: введем вектор 
, связанный с вектором 
невырожденным преобразованием
подобия, заданным матрицей G:
.(5.3)
При этом
матрицу G всегда можно выбрать такой, чтобы матрица 
была жордановой. В матрице по диагонали стоят собственные
числа – корни характеристического уравнения. Жорданова каноническая форма
является удобной, однако, переменные состояния становятся физически не
интерпретируемы.
5.2. Построение модели типа «вход – состояние – выход» для АСР напряжения сварочной дуги
Представим передаточную функцию разомкнутой системы (3.20) в виде произведения простейших сомножителей следующим образом:
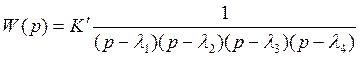(5.4)
Здесь:
(5.5)
Переменные состояния определим следующим образом:
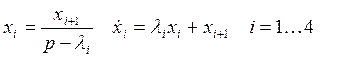(5.6)
Записанная подробно в векторно-матричной форме (5.3) модель данной системы будет иметь вид:
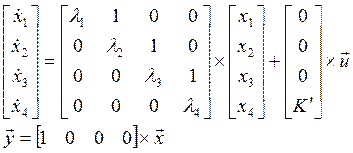(5.7)
На рисунке 15 изображена структурная схема соответствующая такой модели.
 |
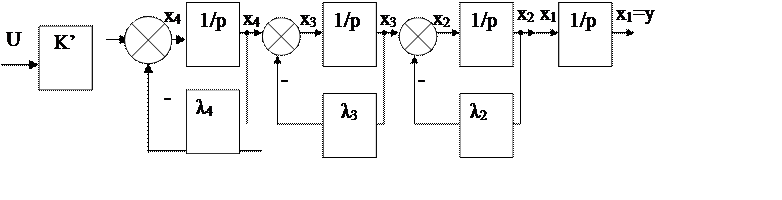Рисунок 15. Структурная схема системы, составленная по модели вход – состояние – выход.
5.3. Исследование свойств управляемости и наблюдаемости.
В данном пункте контрольно-курсовой работы будет рассмотрено соответствие системы критериям управляемости и наблюдаемости, сформулированным Р. Калманом.
Система является полностью управляемой в том случае, если матрица управления Y является матрицей полного ранга. Матрица Y блочная и определяется следующим образом:
(5.8)
Матрицы А и В (состояния и управления соответственно) были определены в пункте 5.2. В соответствии с формулой (5.8):
(5.9)
Очевидно, что Y – квадратная матрица (4*4), то есть данная система будет полностью управляема, если rank(Y)=4. Вычислим матрицу Y, подставив значения из таблицы 1:
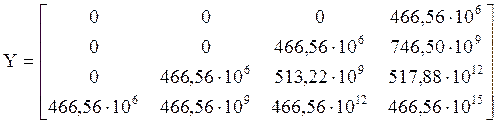(5.10)
(5.11)
Как видно из (5.11) ранг матрицы Y равен 4, таким образом, рассматриваемая система является полностью управляемой.
Для того чтобы выяснить является ли рассматриваемая система полностью наблюдаемой, необходимо проверить, является ли ранг матрицы наблюдения:
(5.12)
полным, то есть проверить условие rank(H)=4. Выполнив необходимые вычисления, получим матрицу H:
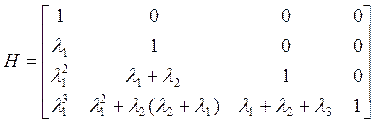(5.13)
Подставив, численные значения получим:
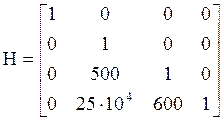(5.14)
(5.15)
Таким образом, система является полностью наблюдаемой.
6. Анализ АСР напряжения сварочной дуги.
6.1. Передаточные функции замкнутой системы.
Ранее были рассмотрены передаточные функции разомкнутой системы, в данном пункте будут определены основные передаточные функции замкнутой системы.
Главный оператор системы:
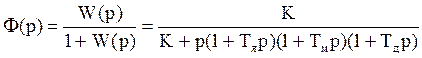(6.1)
Главный оператор дает связь между регулируемой величиной и задающим воздействием, при отсутствии возмущений.
Передаточная функция замкнутой системы по ошибке:
(6.2)
Дает связь между ошибкой и задающим воздействием при отсутствии возмущений.
Передаточная функция замкнутой системы от возмущения по ошибке:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.