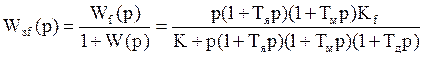Содержательное описание АСР. Описание функциональной схемы. Обоснование способа описания АСР напряжения сварочной дуги, страница 6

                            (6.3)

Дает связь между регулируемой величиной и возмущением (скоростью подачи электрода).

6.2. Исследование устойчивости АСР.

6.2.1. Построение корневого годографа.

Качество системы регулирования с точки зрения быстродействия и запасов устойчивости может характеризоваться расположением корней числителя и знаменателя передаточной функции замкнутой системы.

При плавном изменении какого-либо параметра корни будут перемещаться на комплексной плоскости по некоторой кривой – корневому годографу. Построив траектории всех корней, можно выбрать такое значение варьируемого параметра, что расположение корней будет наилучшим.

Выберем варьируемым параметром общий коэффициент усиления передаточной функции разомкнутой системы. Построение корневого годографа будем производить по методу Эванса. Запишем передаточную функцию разомкнутой системы в виде:

        

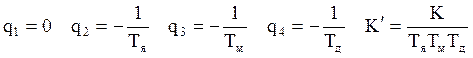          (6.4)

Корневой годограф данной системы будет иметь 4 ветви, начинающиеся при К=0 на вещественной оси, в полюсах разомкнутой системы q. При стремлении коэффициента передачи к бесконечности, ветви стремятся к своим асимптотам (поскольку нулей передаточная функция не имеет, все ветви уходят в бесконечность). Звездную точку выхода асимптот найдем из выражения:

                                                       (6.5)

Углы выхода асимптот:

            (6.6)

 

Рисунок 16. Корневой годограф исследуемой системы.

Точки выхода ветвей корневого годографа найдем из нулевого приращения фаз в точке, бесконечно близко расположенной к точке выхода:

             (6.7)

Решая это уравнение найдем координаты точек выхода α:

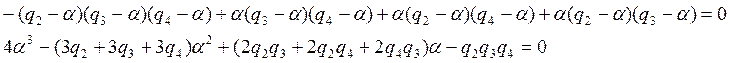
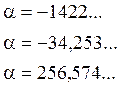                                                             (6.8)

Условием для нахождения точки пересечения корневого годографа с мнимой осью является следующее равенство:

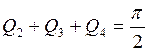                                                        (6.9)

Коэффициент передачи, при котором произойдет пересечение годографа с мнимой осью, получим из равенства:

                                                        (6.10)

Выполнив необходимые, построения получим:

Q₁=90⁰; Q₂=21⁰; Q₃=63⁰; Q₄=6⁰;

r₁=200; r₂=800,2; r₃=330; r₄=1500;

Из (6.10) получим K_пр=1584.

Однако,  в случае систем не выше 3, 4 порядка, для нахождения критического коэффициента передачи удобнее пользоваться косвенными методами.

6.2.2. Исследование устойчивости косвенными методами

6.2.2.1. Критерий Гурвица

Вычисление корней характеристического уравнения выше 3 порядка, уже представляет серьезные трудности. Поэтому желательно иметь такие критерии, с помощью которых можно судить об устойчивости системы по коэффициентам характеристического уравнения. Таким критерием, в частности, является критерий Гурвица.

Характеристическое уравнение АСР, рассматриваемой в данной работе, имеет вид:

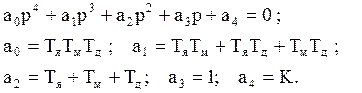  (6.11)

Подставив значения из таблицы 1, получим следующие значения коэффициентов:

Для характеристического уравнения (6.11) составим квадратную матрицу.

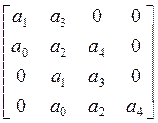                                            (6.12)

Критерий Гурвица сводится к тому, что при a₀>0 должны быть больше нуля все диагональные определители матрицы (6.12). Анализируя эти условия можно получить, что для уравнения четвертого порядка, кроме положительности всех коэффициентов, требуется выполнение условия: 

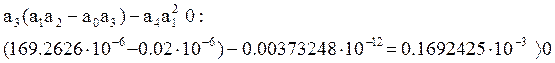        (6.13)

Таким образом, рассматриваемая система удовлетворяет критерию Гурвица, и является устойчивой.

6.2.2.2. Критерий Найквиста и определение запасов устойчивости

Разомкнутая система находится на границе устойчивости, характеристическое уравнение (многочлен в знаменателе) имеет нулевой корень, как следствие астатизма. Тогда критерий Найквиста для такой системы будет сформулирован следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, при изменении ω от 0 до ∞, дополненная на участке разрыва дугой бесконечного радиуса, не охватывала точку с –1 на вещественной оси.

 АФЧХ разомкнутой системы изображена на рисунке 13. Как можно видеть, кривая не охватывает точки [-1,j0], а значит, система удовлетворяет критерию Найквиста, и является устойчивой.