Система также находится на границе устойчивости, если годограф Михайлова начинается из начала координат.
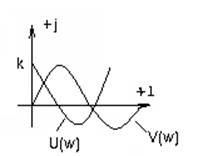
Критерий Михайлова, основанный перемежаемости корней уравнений U(w)=0 и V(w)=0.
![]()

![]()
1) w=0, U(0)=0, V(0)=0
2) w=0, U(w)=k
Если при V’(0)>0 и U(0)>0 система будет устойчивая, корни перемежаются.
Критерий Найквиста.
Критерий Найквиста позволяет определить устойчивость замкнутой системы по годографу или комплексному коэффициенту передачи разомкнутой системы.
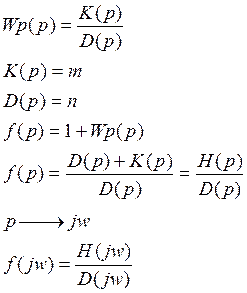 вспомогательная
функция
вспомогательная
функция
Критерий Найквиста для системы устойчивой в разомкнутом состоянии.
![]()
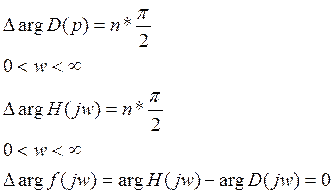
Для устойчивой системы в разомкнутом состоянии замкнутая система будет устойчивая, если изменение аргументов вспомогательной функции будет равна нулю.
Если система в
разомкнутом состоянии была устойчивая, она будет устойчивая и в замкнутом состоянии,
если годограф Wp(w) охватывает точку
[-1; j0] при изменении 0<w<![]()
Пример.
![]()

Определение предельного коэффициента усиления, при котором система будет находиться на границе устойчивости.
![]()
0 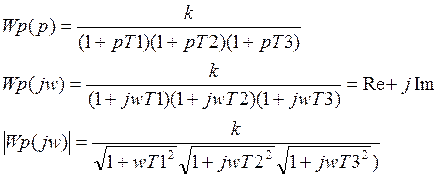
Im(w1)=0
![]() W(w1)=0A
W(w1)=0A
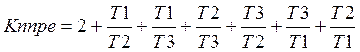
Для нахождения Кпред необходимо приравнять мнимую часть Wp(jw)=0 и найти значение частоты w1 при котором происходит пересечение вещественной оси и найденное значение подставим в выражение модуля Wp(jw) и тем самым определим 0A.
Критерий Найквиста для системы нейтральной в разомкнутом состоянии.
![]()
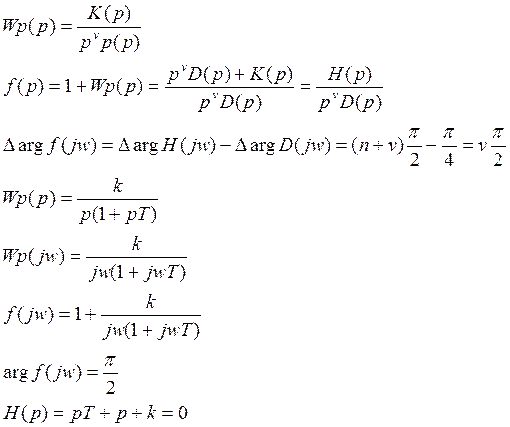
Согласно критерию Найквиста система в замкнутом
состоянии неустойчива, т.к. ![]() .
.
Но с другой стороны по критерию Гурвица система с характеристическим уравнением 2- го порядка устойчива всегда с любым значением k, т.е. получаем противоречие между этими критериями.
Это объясняется тем, что наличие нулевого корня не позволяет точно определить изменение аргумента вспомогательной функции f(w).
Если в разомкнутом состоянии система нейтральная, то в замкнутом она будет устойчивая.
Если годограф Wp(jw) и его дополнения в ![]() не
охватывают точку [-1; j0].
не
охватывают точку [-1; j0].
Дополнение: Если у нас нулевой корень
кратности v, то его надо дополнять ![]() частями
окружности, бесконечно большого радиуса.
частями
окружности, бесконечно большого радиуса.
Пример 1.
![]()
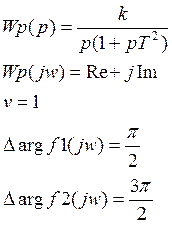
![]() Пример 2.
Пример 2.
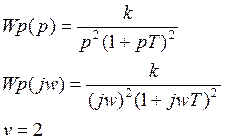
Критерий Найквиста для системы неустойчивой в разомкнутом состоянии.
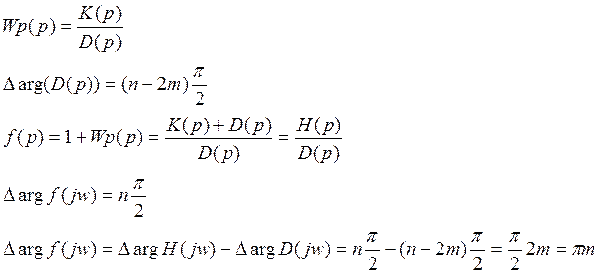
Для того, чтобы система, не устойчивая в
разомкнутом состоянии была устойчивой в замкнутом, необходимо и достаточно,
чтобы изменение аргумента вспомогательной функции = m![]() , где
, где
m- число пр. корней характеристического уравнения, разомкнутой системы D(p)=0.
Для того, чтобы неустойчивая в разомкнутом
состоянии система стала устойчивой в замкнутом состоянии, необходимо и
достаточно, чтобы годограф Wp(jw)
охватила бы точку [-1; j0] в положительном направлении в ![]() раз.
раз.
Практический критерий Найквиста.
![]()
Если годограф пересекает (![]() ;
-1) сверху вниз, то
такой переход называется положительным.
;
-1) сверху вниз, то
такой переход называется положительным.
Если годограф пересекает (![]() ;
-1) снизу вверх, то
такой переход называется отрицательным.
;
-1) снизу вверх, то
такой переход называется отрицательным.
Если годограф не охватывает точку (-1; j0), то система в замкнутом состоянии будет устойчивая.
Система будет устойчивой в замкнутом
состоянии, если разность между количеством положительных и отрицательных
переходов годографа Wp(jw) на участке
(-j; -1) с дополнением в ![]() при
увеличении частоты от 0 до
при
увеличении частоты от 0 до ![]() равнялось
бы
равнялось
бы ![]() раз, где m – число корней характеристического уравнения разомкнутой системы.
раз, где m – число корней характеристического уравнения разомкнутой системы.
Критерий Найквиста, основанный на построении ЛФЧХ.
![]()
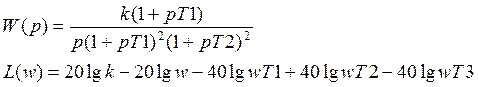
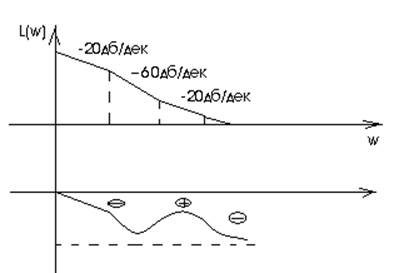
Условимся обозначать отрицательный переход
ЛФЧХ прямых ![]() сверху
вниз.
сверху
вниз.
Для того, чтобы система была устойчивая в
замкнутом состоянии, необходимо и достаточно, чтобы разность между
отрицательным и положительным переходами логарифмические характеристики при возрастании
частоты от 0 до ![]() было
бы равно
было
бы равно ![]() раз.
раз.
Существуют запасы устойчивости по фазе и амплитуде.
Определение запаса устойчивости по годографу разомкнутой системы.
![]()
![]()
1)
![]()
2)
![]()
![]() - запас по
фазе
- запас по
фазе
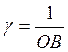 - запас
по амплитуде
- запас
по амплитуде
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.