Задача автоматического регулирования. Объект регулирования. Регулируемая величина. Уставка и регулятор. Система регулирования, страница 6

Определение предельного коэффициента усиления статической системы, в разомкнутом контуре которого находится три инерционных звена.

Значение к, при котором система находится на границе устойчивости, называется предельным

 

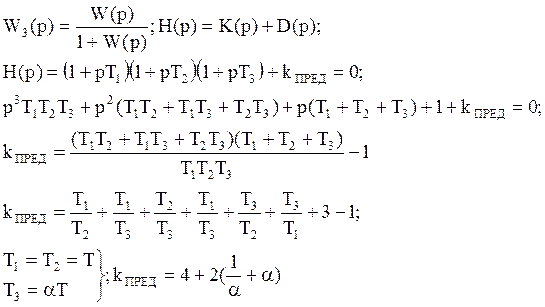
Если имеются 3 одинаковых постоянных времени, то она обладает устойчивостью при .

При

При

Для повышения устойчивости системы необходимо разнести постоянные времени.

Разнесение постоянных времени в статической системе 3-го порядка. Способ увеличения устойчивости.

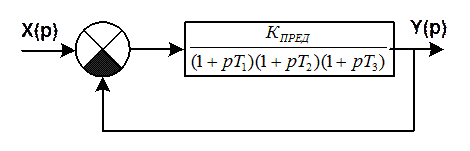
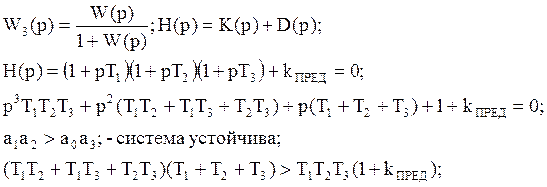
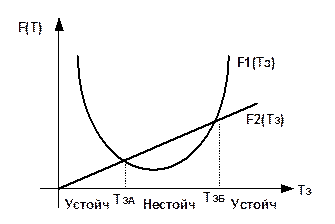
Если  и  в случае равенства система будет находиться на границе устойчивости.

Если , то система стремится стать системой 2-го порядка, а система 2-го порядка всегда устойчива при любом k (коэффициенты при этом должны быть положительными).

Если , то система стремится к системе 1-го порядка, которая всегда устойчивая. Следовательно, для улучшения устойчивости системы необходимо разносить постоянные времени.

Определение k_пред в астатической системе 3-го порядка.

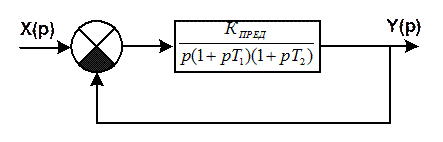
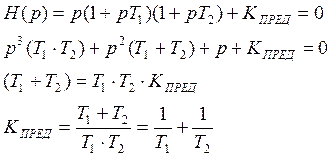
Критический коэффициент в астатической системе определяется абсолютными значениями постоянных времени и для увеличения Кпред необходимо уменьшать абсолютные значения постоянных времени.

Способы изменения постоянных времени инерционных звеньев.

·  Охват инерционного звена жесткой ОС.

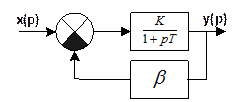
Охват жесткой ОС интегрирующего звена изменяет постоянную времени в (1+) раз.

·  Охват инерционного звена гибкой ОС.

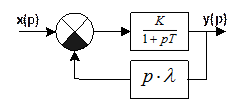
Охват гибкой связью увеличивает постоянную времени.

·  Охват 2-х инерционных звеньев гибкой ОС.

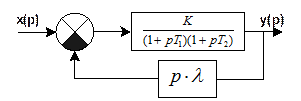
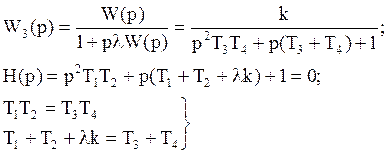
Вывод: При охвате 2-х инерционных звеньев гибкой ОС постоянные времени разносятся, т.е. удаляются друг от друга.

Частотные методы анализа устойчивости. Принцип аргумента.

Частотные методы анализа устойчивости основаны на принципе аргумента:

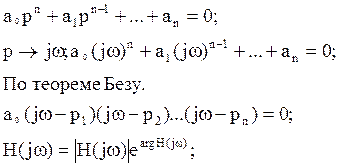
Поскольку  не может быть отрицательной, то в нашем случае:

1.  Если корни вещественные и находятся в левой полуплоскости, то изменение аргумента            ( от 0 до ) =

2.  Если корни вещественные и находится в правой полуплоскости, то изменение аргумента       ( от 0 до ) =

3.  Если корни комплексные и находятся в левой полуплоскости, то изменение аргумента           ( от 0 до ) =

4.  Если корни комплексные и находятся в правой полуплоскости, то изменение аргумента         ( от 0 до ) =

Если имеется n-корней при этом m-корней лежит в правой полуплоскости, тогда полное изменение аргумента при изменения  от 0 до  будет иметь следующее выражение.

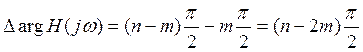
Критерий Михайлова.

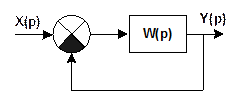
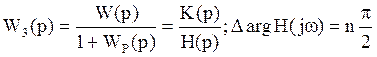
Чтобы система была устойчивой в замкнутом состоянии необходимо и достаточно,  чтобы изменение аргумента характеристического многочлена при изменении  от 0 до  равнялось бы  в положительном направлении.

Геометрическая интерпретация критерия Михайлова.

                                   

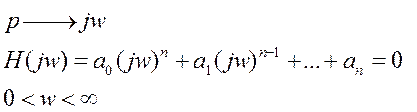
Для того, чтобы система была устойчивой в замкнутом состоянии необходимо и достаточно, чтобы вектор Михайлова начинался на положительной части действительной оси и  при изменении

0<w< прошел бы  в положительном направлении n квадрантов.

Пример 1.

                           

n=1        
                                                                                               1+k

Пример 2.

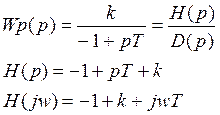                                                               k=1

-1+k

k< система неустойчивая

k=1 на границе устойчивости

Пример 3.

n=5 система устойчива

Признаки неустойчивости системы по критерию Михайлова.

а)система не устойчива начинается на отрицательной части.

k

б)                                                     система не устойчива нарушен порядок чередования.

в)                                                    система не устойчива меняется направление.

г) система на границе устойчивости д)

система на границе устойчивости

Система находится на границе устойчивости, если годограф Михайлова проходит через начало координат. В этом случаи имеется пара комплексных корней, лежащих на мнимой оси.