Задача автоматического регулирования. Объект регулирования. Регулируемая величина. Уставка и регулятор. Система регулирования, страница 4

5.  Направление ветвления. Перенос звеньев по и против направления ветвления.

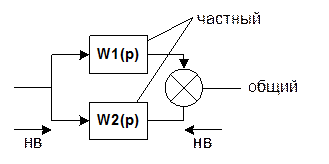
а)  При переносе звеньев по направлению ветвления из общего канала в частный ставятся звенья с передаточной функцией переносимого звена.

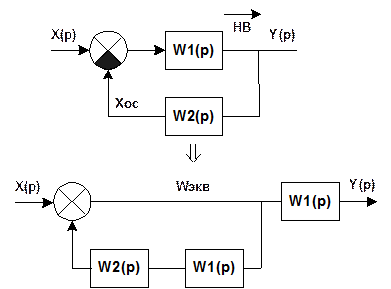
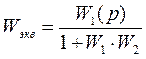
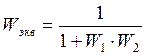
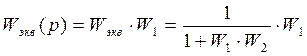
б)  При переносе звена из частного канала против направления ветвления необходимо поставить общий канал звена с передаточной функцией переносимого звена, а в другой – частные каналы звена с функцией обратной передаточной функции переносимого звена.

Вывод: При преобразовании структурной схемы нужно помнить, что основные соотношения между системами преобразованного участка схемы до преобразования  должен сохраняться и после преобразования.

Пример:

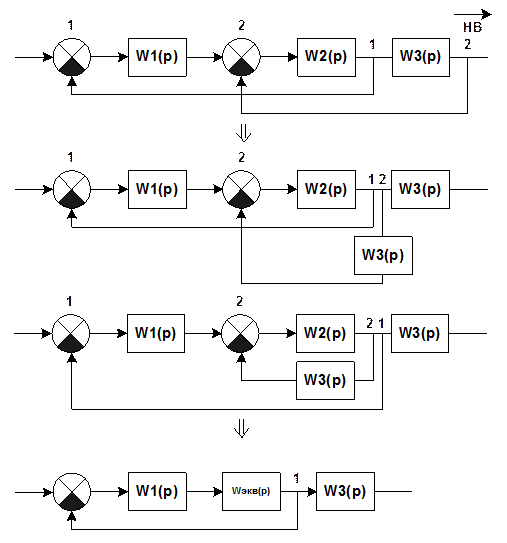
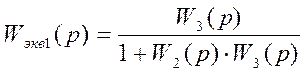
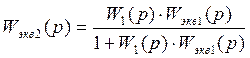
Передаточная функция по ошибке.

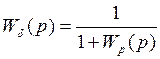
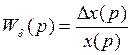
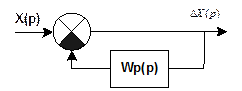
Составление структурной схемы ОУ.

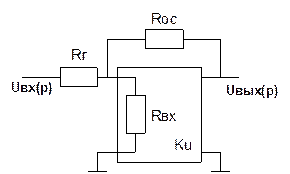
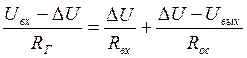
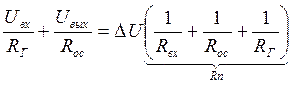
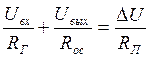
(1)

   

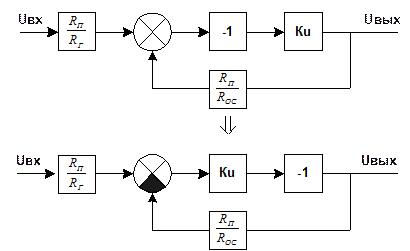
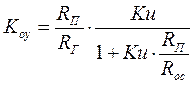
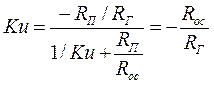
Комплексный коэффициент передачи.

                        
                          

 - амплитудно-частотная характеристика – АФХ.

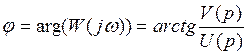  -  фазо-частотная характеристика – ФЧХ.

Пример 1.

Пример 2.

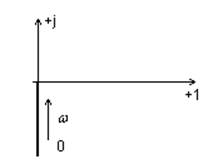
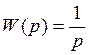
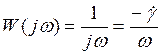
Пример 3.

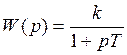
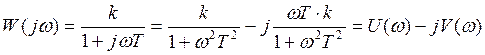
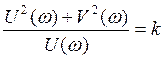
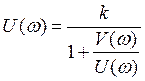
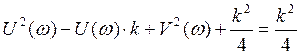
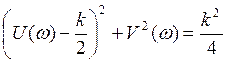
Три формы оператора.

1. Если x  и  y – функции времени, то имеем обыкновенный дифференциальный оператор.
2. Если х  и  у – изображение сигналов, то имеем оператор в преобразовании  Лапласа или передаточную функцию.
3. Если сигналы х и у представлены в виде частотного спектра jω, то имеем комплексный коэффициент передачи.

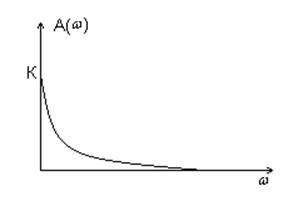
Частотные характеристики системы.

1)  Амплитудно-частотная характеристика.

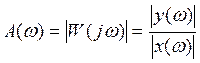
2)  ФЧХ

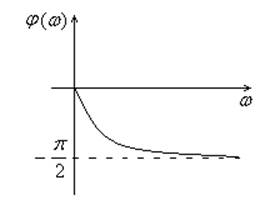
 Пример 1.

            

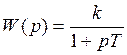
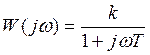
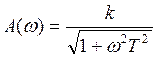
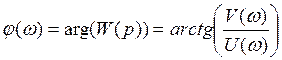
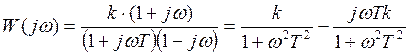
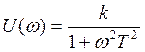
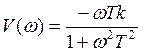
Пример 2.

 

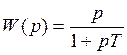
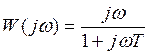
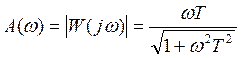
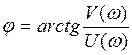
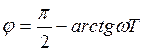
Логарифмические частотные характеристики.

1. Логарифмическая АЧХ.

2. Логарифмическая ФЧХ.

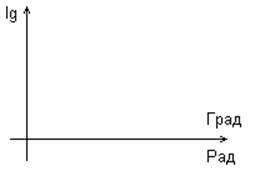
Пример.

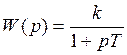
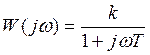
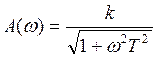
1.      

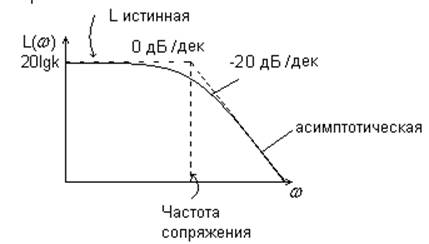
2.                   

                      

   
                                                        

Правила построения ЛАЧХ.

1.  Находятся частоты сопряжения асимптотических ЛАЧХ. Число частот в сопряжении, как правило, определяется количеством нулей и полюсов передаточной функции.

2.  На оси частот наносятся значения сопрягающих частот.

3.  Рассматриваются диапазоны частот от 0 до ω₁ , где ω₁ – наименьшая частота сопряжения, а выражение пренебрегается значение 1 и записывается в выражение для 1-й  асимптоты.

4.  Рассматривается 2-й диапазон частот от  ω₁  до ω₂ , где ω₂ – 2-я сопрягающая частота, выражение пренебрегается 1 и т.д.

5.  При построении ФЧХ положение оси аргумента является плавающим, т.к. нельзя провести через точку ω = 0 ось.

Пример.

                      

                 

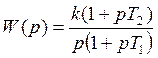
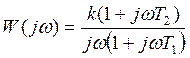
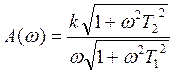
1)   

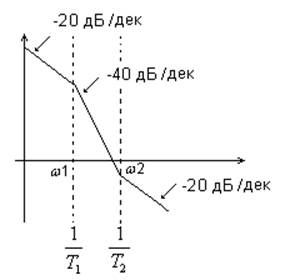
2)    

3)     

Типовые звенья автоматических систем

1.  Пропорциональное звено

                 

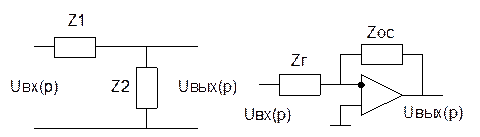
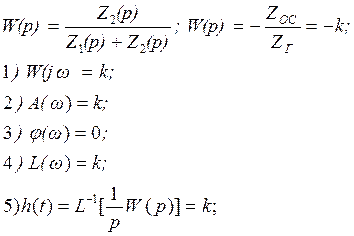
2.  Интегрирующее звено

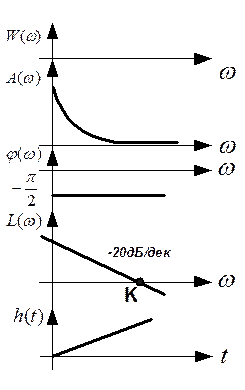
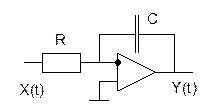
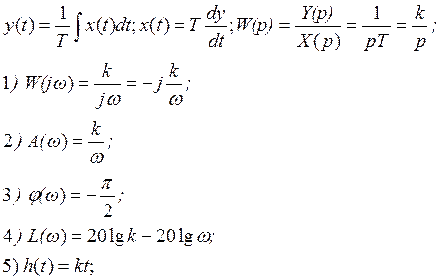
3.  Инерционное звено

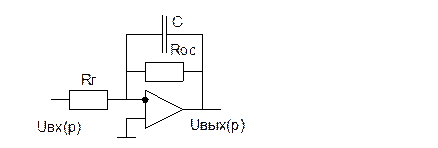
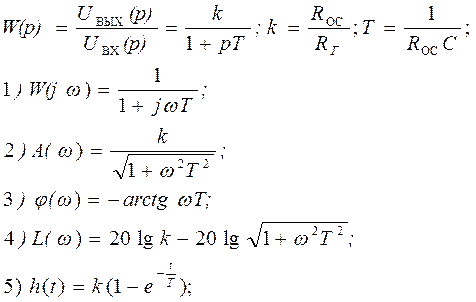
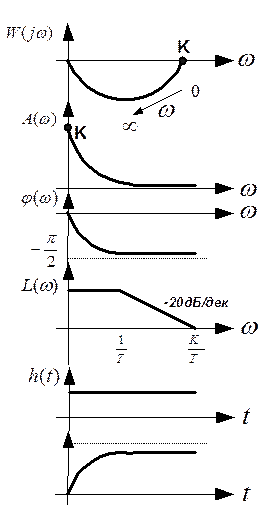
Способы определения времени инерционного звена.

1.  Способ касательной

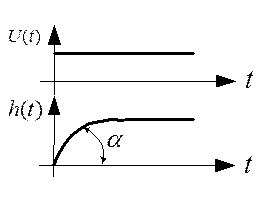
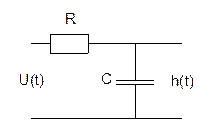
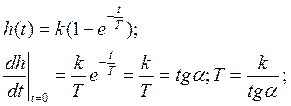
2.  Метод определения по уровню 0,63.

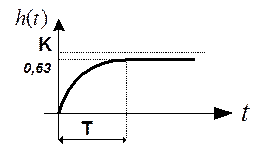
3.  Частотный способ

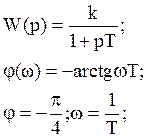
Идеальное дифференцирующее звено.

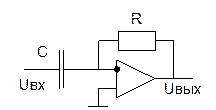
Реальное дифференцирующее звено.

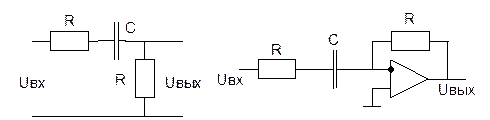
Форсирующее звено.

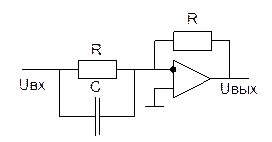
Колебательное звено.

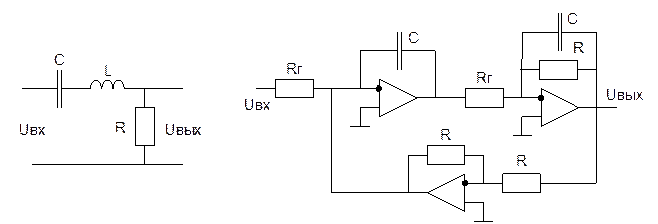
Консервативное звено.

Звено запаздывания.

Теорема Боде.

-текущее значение частоты

-частота, на которой определяется ФЧX.

Теорема Боде применяется для асимптотических ЛАЧХ и дает приближенное качественное значение фазовой характеристики (в точках излома фазовая характеристика будет соответствовать истинному значению, если частота излома асимптоты ЛАЧХ расположены друг от друга на расстоянии не менее одной декады).

На частоте излома ЛАЧХ фазовая характеристика принимает предельное значение фазового сдвига предыдущего участка ЛАЧХ + половина фазового сдвига включаемого участка ЛАЧХ.

Пример

Передаточные функции разомкнутых систем.

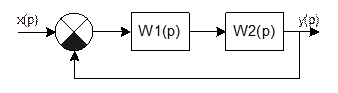
-характеристическое уравнение.

Устойчивость автоматических систем.