Задача автоматического регулирования. Объект регулирования. Регулируемая величина. Уставка и регулятор. Система регулирования, страница 5

Пусть система при неизменных входных и выходных сигналах находится в состоянии покоя. Тогда, если x(t) начнет изменяться и через некоторое время придет в первоначальное состояние, то выходная координата будет изменяться. И если она вернется в прежнее состояние, то можно говорить, что система устойчива. Если же система не вернется в прежнее состояние, то говорят, что система нейтральная

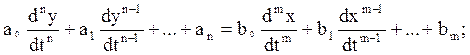
Принужденная составляющая в основном определяется характеристикой входного сигнала, а свободная определяется решение дифференциального уравнения от левой части.

Система устойчива:

Система нейтральна:

Система неустойчива:

Достаточные условия устойчивости.

Достаточным условием устойчивости системы является расположение корней в левой полуплоскости. Если хотя бы один корень расположен в правой полуплоскости, то такая система неустойчива. Если вещественные или комплексно сопряженные корни расположены на мнимой оси, то система называется нейтральной или же находится на границе устойчивости.

Необходимое условие точности.

Если система устойчива, то коэффициенты характеристического уравнения положительны.

Обратное утверждение не всегда верно! Если хотя бы один коэффициент отрицателен, то система неустойчива.

 Теорема Безу

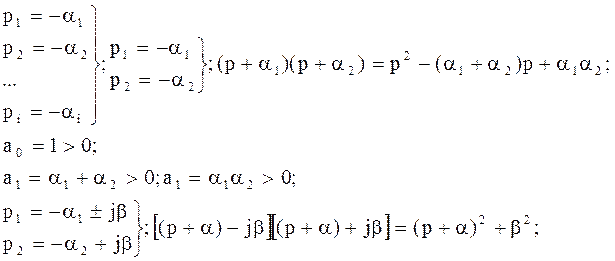
Анализ устойчивости системы 1-го и 2-го порядка.

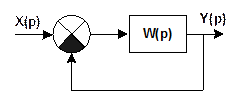
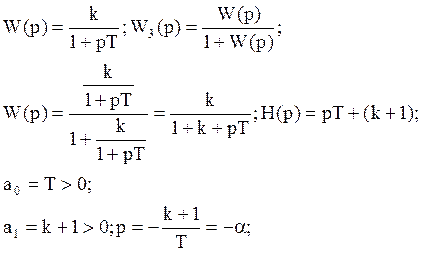
Для систем 1-го порядка необходимое условие является и достаточным.

Для систем 2-го порядка необходимое условие является и достаточным.

Критерии устойчивости.

Правила позволяющие определить расположение корней характеристического уравнения на комплексной плоскости относительно мнимой оси называются критерием устойчивости. Будем рассматривать алгебраический критерий устойчивости, к которому относятся критерий Рауса и критерий Гурвица, а также частотный критерий устойчивости – критерии Михайлова и Найквиста.

Критерий Рауса.

При  применяют критерий Гурвица

При  применяют критерий Рауса.

	1	2	3	…
				…
			…	…
		…	…	…
…	…	…	…	…

Система будет устойчива в замкнутом состоянии, если все коэффициенты первого столбца таблицы Рауса будут положительными. Если хотя бы один коэффициент первого столбца отрицателен, то система неустойчива. Число корней характеристического уравнения, лежащих в правой полуплоскости определяется количеством смен знака у первого столбца.

Критерия Гурвица.

Для того, чтобы воспользоваться правилом Гурвица составим таблицу:

       

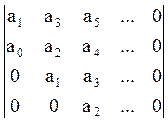
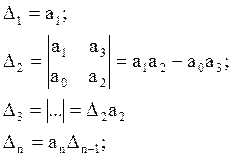
Таблица Гурвица составляется следующим образом:

В первой строке записываются коэффициенты с нечетными индексами, во второй – с нечетными.     Третья строка – смещение 1-ой на 1 коэффициент вправо, 4-ая – смещение 2-ой на 1 коэффициент вправо и т.д.

Система будет устойчивой, если все определители Гурвица положительные при первом положительном коэффициенте а₀. Если хотя бы один определитель <0, то система неустойчива.

Определение количества определителей Гурвица, подлежащих проверке, при анализе устойчивости.

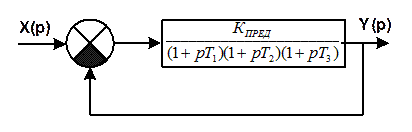
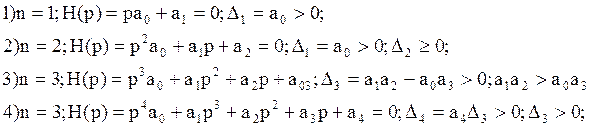
Замечания:

1.  Критерий Гурвица для определения устойчивости системы () как правило не определяется.

2.  Для системы 3-го порядка система будет устойчива если произведение средних коэффициентов больше произведения крайних.

3.  Если , то в характеристическом уравнении имеется один нулевой корень и система находится на границе апериодической устойчивости.

4.  Если определитель n-1 порядка равен 0, то это значит, что имеется пара комплексных корней лежащих на мнимой оси, то система находится на границе колебательной устойчивости.