Возмущение, приложенное после интегрирующего элемента, будет отбрасываться с точностью до зоны нечувствительности. А возмущение, приложенное до интегрирующего элемента в реальной системе, будет приводить к изменению зоны чувствительности приведенным по входу системы. Поэтому в астатической системе необходим коэффициент усиления усилителя (выбирают по заданному значению зоны нечувствительности).
Влияние помех в астатических системах регулирования.
=
ω = 0; α = const
=
= 
=
()·
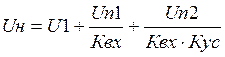
Помехи, приложенные до интегрирующего усилителя в астатических системах такие же как и в статических.
Уравнения движения системы.
Если задать изменения XВХ (t), то у нас на выходе появиться Y(t), и система придет в движение.
С математической точки зрения система преобразует одну функцию времени в другую. Соотношение в каждый момент времени между входными и выходными координатами сохраняется и образует систему линейных уравнений.
Система должна быть полной и тогда, путем исключения нелинейных координат находят уравнения движения системы, представляющие зависимость между обобщенными координатами.
Математически выходная координата может быть получена, если использовать оператор преобразования. Оператором называется закон, в соответствии с которым по заданной функции находится выходная функция.
Оператор – совокупность математических действий, которые необходимо применить над входной функцией для получения выходной.
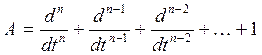
Линеанизация системы.
В общем случае система регулируемая является нелинейной. Во многих случаях система работает с малыми изменениями координат от установленного режима. В этом случае нелинейные дифференциальные уравнения могут быть линеанизированы, т.е. заменены линейными дифференциальными уравнениями.
Принцип замены нелинейных дифференциальных уравнений линейными называется линенизацией.
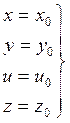
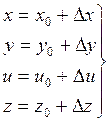
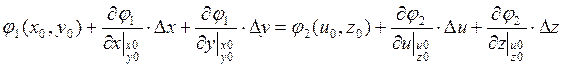
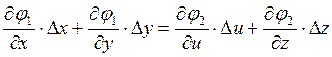
Вывод:
1. Это уравнение превращения координат.
2. Это приближенное уравнение, т.к. высшими членами в разложении в ряд Тейлора мы пренебрегаем.
3. Это линейные уравнения относительно приращения.
Преобразование Лапласа.
Преобразуется функция действительного переменного в функцию комплексного. При этом дифференциальные уравнения заменяются алгебраическими уравнениями. Некоторая функция f(t):
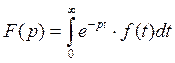
Свойства линейности:
1. 
a) 
б) 
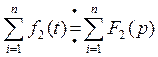
2. Теорема запаздывания.
3.
4. Теорема об интегрировании (теорема коррелирования).
5. Теорема о начальном значении функции.
6. Теорема о конечном значении функции.
7. Теорема о свертке.
8. 
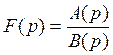
а)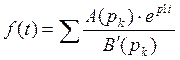 
, где 
- корни
уравнения 
б)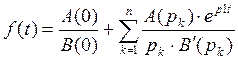 
Пример:
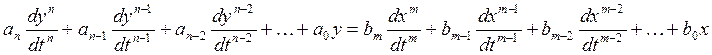
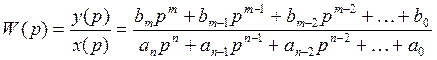
Передаточная функция ОУ.
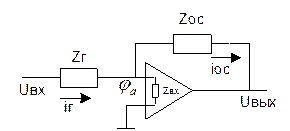
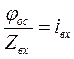
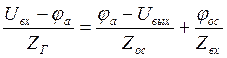
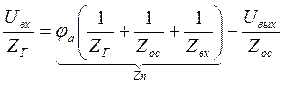
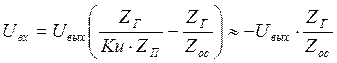
>>1
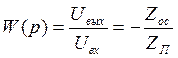
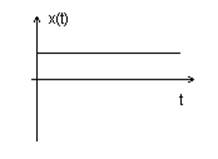
Переходная функция системы.
Переходная функция системы – реакция системы на единичный скачок при условии, что до момента подачи скачка система находилась в покое.
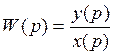
Пример.
Дано:
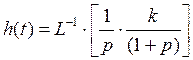
Алгебра структурной схемы.
Правило преобразования структурной схемы.
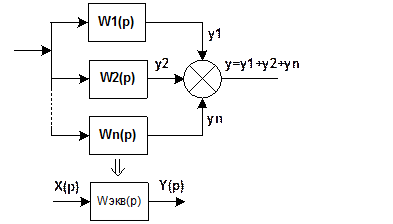
Структурная схема может быть представлена в виде соединений однонаправленных звеньев.
Однонаправленное звено – выходной сигнал, который зависит только от входной величины, не зависит и не изменяется от подключенной нагрузки на выход данного звена.
Правило соединения:
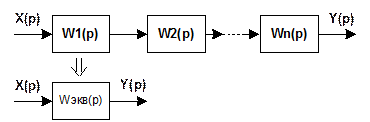
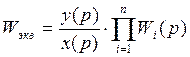
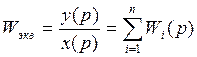
Понятие о гибкой и жесткой ОС.
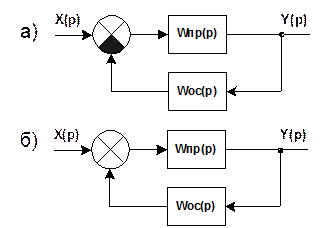
Жесткая ОС – связь, при которой сигнал звена ОС проходит сумматор как в переходном, так и в режиме статики.
Гибкая ОС – такое звено, у которого сумматор сигнал проходит только в переходном режиме.
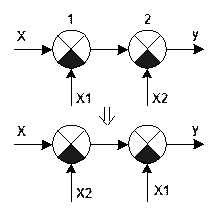Смена узлов у сумматора.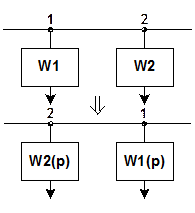
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.