Информатика и выч. техника \ Информационные системы в экономике

Разработка проекта информационной системы интернет-обслуживания клиентов компании ООО. Отображение детализированного отчета звонков с номеров пользователя, страница 7

В любой информационной системе задача состоит в достижении максимальной достоверности передачи информации. Достоверность информации определяется как степень адекватного отображения информацией объективно существующих явлений, событий или процессов.

Достоверность связана с вероятностью возникновения ошибок. Под ошибкой понимается случайное событие - искажение информации, которое может быть обнаружено и зарегистрировано с определенной вероятностью.

Для расчета достоверности применяются различные математические и логические приемы выявления ошибок, включаемые в компьютерные программы, а также многократное повторение передачи одинаковых данных.

Для проекта №1:

Требуется рассчитать достоверность информации для задачи ввода информации о клиенте в базу данных оператором. Достоверность информации должна быть не меньше 0,999 после каждого техпроцесса рассматриваемой задачи.

Изобразим схему внесения информации в БД:

Рис.2.4.1 Схема внесения информации в БД

1)  Вероятность искажения информации при ручном вводе с клавиатуры

2)  Вероятность обнаружения ошибки оператором при самоконтроле

3)  Интенсивность сбоев сервера БД 

4)  Интенсивность сбоев ЛВС 

5)  Объем вводимых символов:

Таблица 2.4.1 Объем вводимых символов

Наименование поля

Длина, байт

Код клиента

10

Имя

20

Фамилия

30

Отчество

30

Номер телефона

15

Адрес

45

Итого

150

Примем Q = 170 (с учетом преамбулы, адреса получателя и отправителя, поля контрольной суммы).

1.  Пропускная способность сегмента 100 BaseTX – 95 мбит/с

2.  Пропускная способность коммутатора HP 2530-48G - 104 Гбит/сек

3.  Доступ к жесткому диску 8,5 мс

4.  Скорость записи 500 Мбит/с

1)  Сделаем расчет достоверности для ручной операции ввода сведений о новом клиенте.

Вероятность искажения информации после выполнения ручной операции ввода при условии независимой посимвольной обработки определяется как:

,

Где qi – вероятность искажения единицы обрабатываемой информации,

Qi – объем единиц обрабатываемой информации.

Достоверность обработки информации в таком случае:

0,84359306

Введем схему контроля ошибок при ручном вводе:

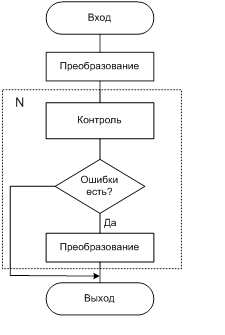
Рис.2.4.2 Схема контроля ошибок при ручном вводе

Тогда полная вероятность поступления искаженного символа данных на выход алгоритма вычисляется по формуле умножения вероятностей:

k – вероятность обнаружения ошибки при контроле,

r – вероятность внесения ошибки после выполнения корректирующей операции,

N – количество операций контроля

0,031406513

0,968593487

0,006306428

0,993693572

0,001266331

0,998733669

0,000254279

0,999745721

Таким образом, для достижения допустимого значения достоверности 0,999 операции ввода данных с клавиатуры применим четырехкратный контроль.

2)  Передача данных по ЛВС

Уточним модель достоверности для операции передачи информации по ЛВС:

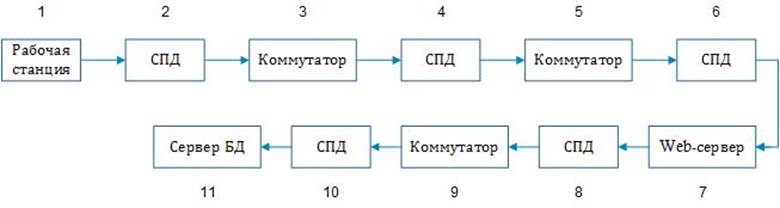
Рис.2.4.3 Модель достоверности для операции передачи информации по ЛВС

В случае машинной обработки информации применяется эмпирическая формула для расчета вероятности отсутствия ошибки после операции:

p = e-10λt

где  10λ – интенсивность сбоев технических устройств;

t  - время обработки.

Рассчитаем время t передачи пакета длиной 170 байт = 1360 бит по узлам сети:

100Base-TX = 1360 бит / 100 Мбит/с = 13,6*10-6 с

HP 2530-48G= 1360 бит / 104 Гбит/с = 0,013*10-6 с

Web-сервер = 0,0015 с

t = 13,6*10-6 + 0,013*10-6 + 13,6*10-6 + 0,013*10-6 + 13,6*10-6 + 0,0015 + 13,6*10-6 + 0,013*10-6 + 13,6*10-6 = 0,001568039 с

λ = 0,001 1/час = 0,001/3600с = 2,78*10-7 1/с

P2 = e^(-10 * 2,78*10-7 * 0,001568039)

3)  Уточним модель достоверности для операции сохранения информации на сервере БД:

10* – интенсивность сбоев технических устройств,

t – время обработки.

 = 1/час = /3600с = 1,06*10-8 1/с

T = Tдост + Tзаписи = 8,5*10-3 с + 3600 бит / 500*106 бит/с = 0,0085 c

Скачать файл