Разработка проекта информационной системы интернет-обслуживания клиентов компании ООО. Отображение детализированного отчета звонков с номеров пользователя, страница 5

Итого:

Стоимость проекта №3:  400 826 руб.

2.3.  Расчет надежности комплекса технических средств

Для оценки вероятности сбоев информационной системы интернет-обслуживания клиентов компании ООО «Система-» необходимо рассчитать и оценить надёжность комплекса технических средств системы.

Для расчета надежности технические устройства информационных систем (структурные модели) заменяются адекватными моделями надежности. При этом в структурной модели выделяют элементы, определяющие способность выполнять свои функции и тем самым влияющие на надежность (существенные элементы). Затем существенные элементы соединяются в некоторую структуру. Это соединение будет последовательным (последовательная модель надежности), если отказ хотя бы одного элемента системы приводит к отказу всей системы.

Отказ – переход системы в ненадежное состояние. Порядок элементов в последовательной модели не существенен с точки зрения надежности. Исходная модель надежности технического обеспечения информационных систем на укрупненном уровне детализации является, как правило, последовательной. Если показатели надежности последовательной модели не удовлетворяют заданным требованиям, то необходимо изменить структурную модель (например, ввести избыточные элементы) и перейти к рассмотрению другой модели надежности. Это может быть параллельная модель, параллельно-последовательная или другая.

Все составляющие структурной модели комплекса технических средств информационной системы будем рассматривать как восстанавливаемые элементы (используемые многократно). В качестве количественного показателя надежности КТС примем функцию готовности (вероятность события, состоящего в том, что КТС обеспечивает выполнение решения конкретной задачи в момент времени t).

Для нахождения функции готовности необходима интенсивность отказов и интенсивность восстановления.

Рассчитаем надежность для задачи ввода информации об услугах клиента в базу данных оператором.

Для проекта №1:

Рис.2.3.1 Структурная схема надежности

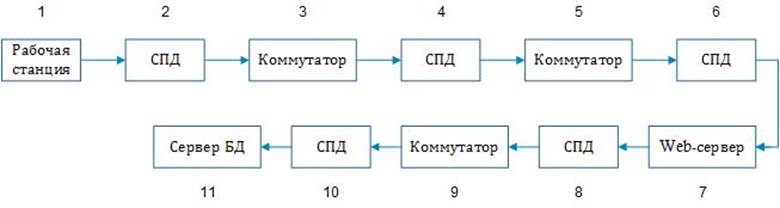
Рис.2.3.2 Последовательная модель надежности

Интенсивности отказов и восстановления элементов:

1.  Рабочая станция (гарантийный срок = 3 года):

 = 1/ 26280ч = 0,000038052 (1/ч)

 = 1/ 2 = 0,5 (1/ч)

2.  СПД:

 =  = (1/ч)

 =  =  =  =  = 1 (1/ч)

3.  Коммутатор (гарантийный срок = 1 год):

 =  =  = 1/8760ч = 0,0001142 (1/ч)

 =   =   = 1 (1/ч)

4.  Web-сервер (гарантийный срок = 3 года):

 = 1/ 26280ч = 0,000038052 (1/ч)

 = 1 (1/ч)

5.  Сервер БД (гарантийный срок = 3 года):

 = 1/ 26280ч = 0,000038052 (1/ч)

 = 1 (1/ч)

• пуассоновский поток отказов
• время восстановления элемента распределяется по экспоненциальному закону
• расчетный период t= 5 лет = 43824ч
• допустимая для задачи вероятность сбоев g_доп=0,999   

Вероятность того, что в момент времени t i-ый элемент находится в рабочем состоянии, определяется функцией готовности:

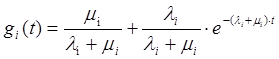
g₁(t) = 0,999961949

g₂(t) = 0,999000999

g₃(t) = 0,999885813

g₄(t) = 0,999000999

g₅(t) = 0,999885813

g₆(t) = 0,999000999

g₇(t) = 0,999961949

g₈(t) = 0,999000999

g₉(t) = 0,999885813

g₁₀(t) = 0,999000999

g₁₁(t) = 0,999961949

Вероятность того, что в момент времени t КТС находится в рабочем состоянии, определяется как произведение функций готовности элементов:

g(t) =

g(t) = 0,994560611

G(t)<0,999. Следовательно, полученное значение не удовлетворяет заданному требованию.

Воспользуемся введением избыточных параллельных блоков для элементов с наименьшей надежностью ,, , , . Основные и резервные блоки имеют одинаковые интенсивности отказов и восстановления.

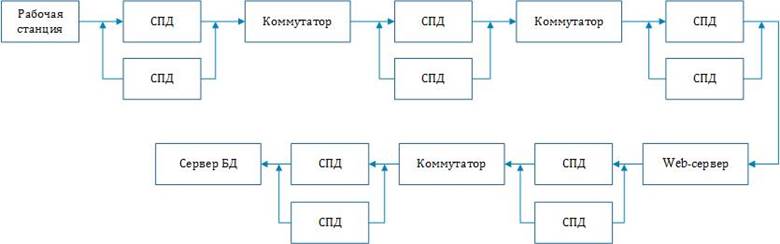
Рис.2.3.3 Последовательно-параллельная модель надежности (холодный резерв)

Вычислим g(t) для параллельных элементов:

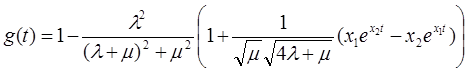, где

,  

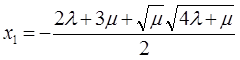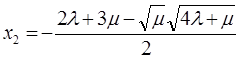
-2,001999002

-1,000000998

g ₂(t)= g₄(t)= g ₆(t)= g₈(t)= g₁₀(t)= 0,9999995

G(t)= 0,999540874 > 0,999

Следовательно, с помощью ввода дополнительных элементов, мы получаем удовлетворяющую условию задачи функцию готовности.

Для проекта №2:

Рис.2.3.4 Структурная схема надежности

Рис.2.3.5 Последовательная модель надежности