Интенсивности отказов и восстановления элементов:
1. Рабочая станция (гарантийный срок = 3 года):
![]() = 1/ 26280ч = 0,000038052 (1/ч)
= 1/ 26280ч = 0,000038052 (1/ч)
![]() = 1
(1/ч)
= 1
(1/ч)
2. СПД:
![]() =
= ![]() =
= ![]() = 0,001 (1/ч)
= 0,001 (1/ч)
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = 1 (1/ч)
= 1 (1/ч)
3. Коммутатор (гарантийный срок = 1 год):
![]() =
= ![]() =
= ![]() = 1/8760ч = 0,0001142
(1/ч)
= 1/8760ч = 0,0001142
(1/ч)
![]() =
=
![]() =
= ![]() = 1
(1/ч)
= 1
(1/ч)
4. Web-сервер (гарантийный срок = 3 года):
![]() = 1/ 26280ч = 0,000038052 (1/ч)
= 1/ 26280ч = 0,000038052 (1/ч)
![]() = 1
(1/ч)
= 1
(1/ч)
5. Сервер БД (гарантийный срок = 1 год):
![]() = 1/8760ч = 0,0001142
(1/ч)
= 1/8760ч = 0,0001142
(1/ч)
![]() = 1
(1/ч)
= 1
(1/ч)
Вероятность того, что в момент времени t i-ый элемент находится в рабочем состоянии, определяется функцией готовности:
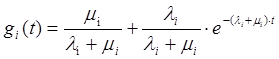
g1(t) = 0,999961949
g2(t) = 0,999000999
g3(t) = 0,999885813
g4(t) = 0,999000999
g5(t) = 0,999885813
g6(t) = 0,999000999
g7(t) = 0,999961949
g8(t) = 0,999000999
g9(t) = 0,999885813
g10(t) = 0,999000999
g11(t) = 0,999885813
Вероятность того, что в момент времени t КТС находится в рабочем состоянии, определяется как произведение функций готовности элементов:
g(t) = ![]()
g(t) = 0,994484886
G(t)<0,999. Следовательно, полученное значение не удовлетворяет заданному требованию.
Воспользуемся
введением избыточных параллельных блоков для элементов с наименьшей надежностью
![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,
![]() .
Основные и резервные блоки имеют одинаковые интенсивности отказов и
восстановления.
.
Основные и резервные блоки имеют одинаковые интенсивности отказов и
восстановления.
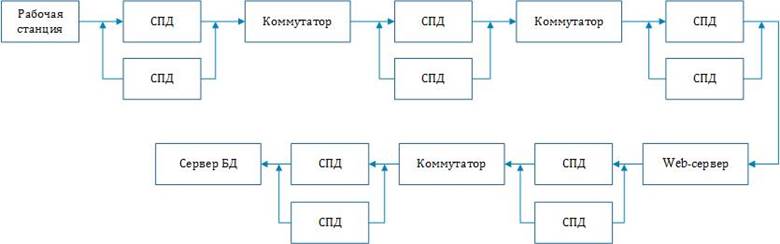
Рис.2.3.6 Последовательно-параллельная модель надежности (холодный резерв)
Вычислим g(t) для параллельных элементов:
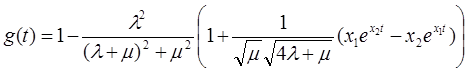 , где
, где
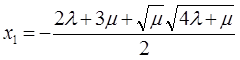 ,
, 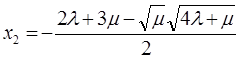
![]() -2,001999002
-2,001999002
![]() -1,000000998
-1,000000998
g 2(t)= g4(t)= g 6(t)= g8(t)= g10(t)= 0,9999995
G(t)= 0,999464769> 0,999
Следовательно, с помощью ввода дополнительных элементов, мы получаем удовлетворяющую условию задачи функцию готовности.
Для проекта №3:

Рис.2.3.7 Структурная схема надежности
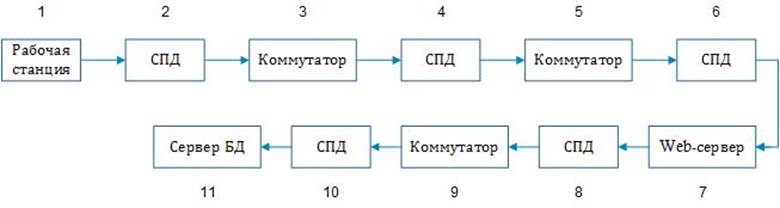
Рис.2.3.8 Последовательная модель надежности
Интенсивности отказов и восстановления элементов:
1. Рабочая станция (гарантийный срок = 3 года):
![]() = 1/ 26280ч = 0,000038052 (1/ч)
= 1/ 26280ч = 0,000038052 (1/ч)
![]() = 1
(1/ч)
= 1
(1/ч)
2. СПД:
![]() =
= ![]() =
= ![]() 0,001 (1/ч)
0,001 (1/ч)
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = 1 (1/ч)
= 1 (1/ч)
3. Коммутатор (гарантийный срок = 5 лет):
![]() =
=
![]() =
=
![]() =
1/43824ч
= 0,0000228 (1/ч)
=
1/43824ч
= 0,0000228 (1/ч)
![]() =
=
![]() =
= ![]() = 1
(1/ч)
= 1
(1/ч)
4. Web-сервер (гарантийный срок = 3 года):
![]() = 1/ 26280ч = 0,000038052 (1/ч)
= 1/ 26280ч = 0,000038052 (1/ч)
![]() = 1
(1/ч)
= 1
(1/ч)
5. Сервер БД (гарантийный срок = 3 года):
![]() = 1/ 26280ч = 0,000038052 (1/ч)
= 1/ 26280ч = 0,000038052 (1/ч)
![]() = 1
(1/ч)
= 1
(1/ч)
Вероятность того, что в момент времени t i-ый элемент находится в рабочем состоянии, определяется функцией готовности:
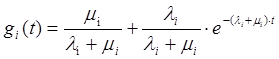
g1(t) = 0,999961949
g2(t) = 0,999000999
g3(t) = 0,999977201
g4(t) = 0,999000999
g5(t) = 0,999977201
g6(t) = 0,999000999
g7(t) = 0,999961949
g8(t) = 0,999000999
g9(t) = 0,999977201
g10(t) = 0,999000999
g11(t) = 0,999961949
Вероятность того, что в момент времени t КТС находится в рабочем состоянии, определяется как произведение функций готовности элементов:
g(t) = ![]()
g(t) = 0,994833339
G(t)<0,999. Следовательно, полученное значение не удовлетворяет заданному требованию.
Воспользуемся
введением избыточных параллельных блоков для элементов с наименьшей надежностью
![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,
![]() .
Основные и резервные блоки имеют одинаковые интенсивности отказов и
восстановления.
.
Основные и резервные блоки имеют одинаковые интенсивности отказов и
восстановления.

Рис.2.3.9 Последовательно-параллельная модель надежности (холодный резерв)
Вычислим g(t) для параллельных элементов:
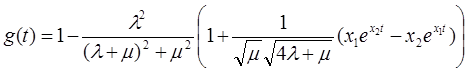 , где
, где
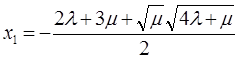 ,
, 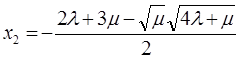
![]() -2,001999002
-2,001999002
![]() -1,000000998
-1,000000998
g 2(t)= g4(t)= g 6(t)= g8(t)= g10(t)= 0,9999995
G(t)= 0,999814967> 0,999
Следовательно, с помощью ввода дополнительных элементов, мы получаем удовлетворяющую условию задачи функцию готовности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.