Законы постоянного тока. Основные определения и формулы. Электрический ток. Сила тока. Дифференциальная форма уравнения непрерывности

ЗАКОНЫ ПОСТОЯННОГО ТОКА

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

Электрический ток  упорядоченный перенос электрического заряда.

Сила тока  заряд, переносимый сквозь рассматриваемую площадь поверхности S в единицу времени: I = ^dQ_dt .

I = _∫ ^!jdS^! , где ^!j  плотность тока.

 уравнение непрерывности.

"_∫ ^!jdS^! = 0  уравнение непрерывности для постоянного тока.

∇ = −!!_j ^∂∂^ρt  дифференциальная форма уравнения непрерывности.

∇ =!!j            0  уравнение стационарности, т.е. в случае постоянного тока поле вектора ^!j не имеет источников.

Закон Ома для однородного проводника: Сила тока, протекающего по однородному проводнику, пропорциональна разности потенциалов на его концах (напряжению U ): I = ^U_R , где R  электрическое сопротивление проводника.

В случае однородного цилиндрического проводника: R = ρ_S^l , где l  длина проводника, S  площадь поперечного сечения, ρ  удельное электрическое сопротивление.

Закон Ома в дифференциальной форме     (локальный закон Ома): ^!j = ρ¹ E^! =σE^! , где σ =   удельная электропроводимость среды.

Обобщенный закон Ома в локальной форме: ^!j =σ(E^! + E^!′), где E^!′  напряженность поля сторонних сил.

Интегральная форма закона Ома для неоднородного участка цепи:

RI =ϕ ϕ₁ − ₂ +ε₁₂ , где ε₁₂  электродвижущая сила.

Правила Кирхгофа:

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: ∑I_k = 0.

Второе правило Кирхгофа: алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивление равна алгебраической сумме ЭДС, действующих в этом контуре: ∑I R_{k k} = ∑ε_k .

Закон Джоуля  Ленца: Q# = RI ² =UI = ^U_R² , где Q#  теплота, выделяемая в единицу времени.

Закон Джоуля  Ленца в локальной форме: удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке: Q#_уд = ρj² , где Q#_уд  удельная тепловая мощность.

Удельная тепловая мощность тока в неоднородной проводящей среде:

Q#_уд = ρj² = ^!j E₍ ^! + E^!′).

Время релаксации  время, за которое заряд конденсатора уменьшается в e раз: τ = RC .

ЗАДАЧИ Правила Кирхгофа:

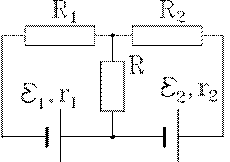1. Сопротивления R₁ и R₂ на схеме заданы. При каком сопротивлении R , выделяемое на нем тепло будет максимальным?

Решение:

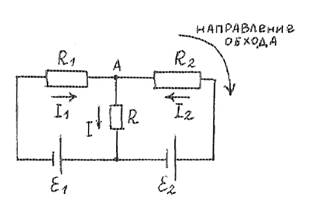
Запишем правила Киргофа:  узел А: I₁ + I₂ = I (1), левый контур: I R_{1 1} + IR = −ε₁ (2), правый контур: −IR − I R_{2 2} = −ε₂ (3);

Джоулево тепло на сопротивлении R равно Q = I Rt² . Ищем I : I₂ = I − I₁ (1), подставляем в (3), получим 

I R_{1 1} + IR = −^ε₁ 2( )      ^,

−I R( + R₂ )+ I R_{1 2} = −ε₂ 3^{( )}

Домножим (2) на R₂ и (3) на (−R₁) и сложим, избавляясь от I₁:

I RR( ₂ + RR₁ + R R_{1 2} )=^{ε ε}₂R₁ ⁻ ₁R₂ , отсюда

I = RR^{ε ε}₂ 2+RRR1 −₁ +1RR R2_{1 2} = RR^{ε ε}₁ +2RR R1 −( ₂1^R2                   ^{=          a}          ,

₊ R₁) b ₊ Rc

a = (ε ε2R1 − 1R2 )2  где  R R_{1 2} = b      . R1 + R2 = c            

Ищем максимум функции I R2 : d I R(dR2 ) = dRd  (R R1(ε ε22R+1R R−(1R1 2+)2RR2 ))2  = 0 или dRd (b +aRcR) ₌ a b( +cR)(²b−+aRcR⋅)24(b +cR c⁾ _{= 0}, т.е.

2

a  b( +cR)−2acR = 0, отсюда R = ^b = ^{R R1 2}  условие максимума выделяемой c R₁ + R₂

мощности на сопротивлении R .

При этом I =               a = ε ε2R1 − 1R2 .

b  + Rc           2b        2R R_{1 2}

Ответ: R = RR R11+ R2 2 .

2.  В цепь моста Уинстона включена э.д.с. с внутренним сопротивлением r = 1 Ом. В двух плечах моста стоят сопротивления R₁ = 1 Ом, R₃ = 2 Ом. Какие сопротивления R₂ и R₄ надо поставить в другие плечи моста, чтобы он был уравновешен (ϕ ϕ_A −        _B = 0) и чтобы в мосте выделялась максимальная мощность?

 Решение:

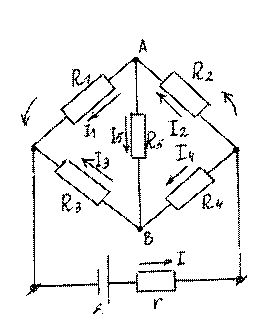
Так как ϕ ϕ_A − _B = 0 (равновесие моста), то I₅ = 0.

Тогда для узлов А и В ^I_I¹3 ⁼₌ ^I_I²4 _^_,

левый верхний контур R I_{1 1} − R I_{3 3} = 0, правый верхний контур R I_{2 2} − R I_{4 4} = 0 .

R^R13 = ^II³1 = ^II2⁴ = ^RR²4 , т.е. условие равновесия моста _R^R3¹ = _R^R4² .

Из условия задачи R₃ = 2R₁, R₄ = 2R₃ .

2

                                        ₂                           ε 

Мощность P = I Rвнеш =  r + Rвнеш  Rвнеш .



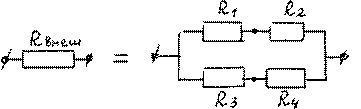
Условие максимума      ^dP         = 0 , R_внеш = r  максимальная мощность во dR_внеш

внешней цепи выделяется, если ее сопротивление равно внутреннему сопротивлению источника, т.е^. _Rвнеш¹ = _R1 ₊¹ _R2 + _R3 ₊¹ _R4 ,

Rвнеш = (RR11 ++ RR22 )(+ RR33 ++ RR44 ) = r , но R3 + R4 = 2(R1 + R2 ), т.е. 23((RR11++RR22))2 = r.

Т.о. R₂ ^{= 3}₂ r − R₁= 0,5 Ом, R₄ = 2R₂ = 1 Ом.

Ответ: R₂ = 0,5 Ом, R₄ = 1 Ом.

3.  В схеме заданы сопротивления R и R₀ и э.д.с. источников ε и ε₀ , а

также емкость C конденсатора. Внутренние сопротивления источников пренебрежимо малы. Найти заряд q на левой обкладке конденсатора.

Может ли этот заряд быть отрицательным?

Решение:

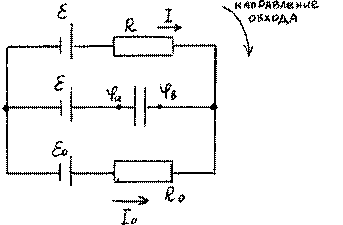
Для внешнего контура RI − R I_{0 0} =ε ε− ₀ .

Т.к. ток через конденсатор не идет, то − =I I₀ , следовательно I = _R^{ε ε−}_{+ R}⁰0 .

Для верхнего контура RI +ϕ ϕ_b − _a =ε ε− ₀ , где ϕ ϕ_b − _a  падение напряжения на конденсаторе ϕ ϕ_a − _b = RI = _{R +}^R_R0 (ε ε− ₀ ).

При ϕ_a > ϕ_b ток I имеет знак «+», при ϕ_a < ϕ_b  наоборот.

Но q = C(ϕ ϕ_a − _b )=   ^CR (ε ε− ₀ ).

R+ R₀

Заряд отрицателен на левой обкладке при ε₀ > ε.

Ответ: q = _R^CR_{+ R}0 (ε ε− ₀ ).

Закон Ома. Нахождение сопротивления:

4.  Сферический конденсатор заполнен однородным диэлектриком с диэлектрической проницаемостью ε и удельным сопротивлением ρ.

Найти сопротивление среды в конденсаторе, если его емкость равна C . Определить напряженность E поля внутри такого конденсатора, если на его обкладки подать напряжение U .