Законы постоянного тока. Основные определения и формулы. Электрический ток. Сила тока. Дифференциальная форма уравнения непрерывности, страница 3

7. К бесконечной металлической плоскости толщиной δ приварены на расстоянии b друг от друга два провода с радиусом a. Найти сопротивление R между проводами, если δ$ $a b. Считать, что удельная проводимость σ_п проводов много больше удельной проводимости σ металла плоскости.

Решение:

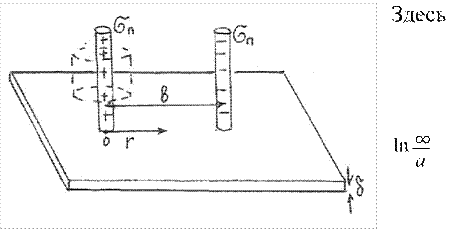считать   проводники раздвинутыми           на      бесконечное расстояние нельзя, иначе получим

= ∞           сопротивление бесконечной плоскости. Т.к. σ σ_п %    , то можно достаточно точно считать, что провода на всей своей длине имеют одинаковый потенциал, т.е. считать, что они заряжены с линейной плотностью зарядов ±λ, одинаковой по всей длине проводника (мысленно).

По теореме Гаусса, окружая провода цилиндрической поверхностью, находим E rl  напряженность поля на оси провода.

Т.е. на удалении r от оси левого провода E r( ) = E_лев + E_прав = 2_πε^λ 0 _^{ 1}_r + _b¹_−r ^_ .

 

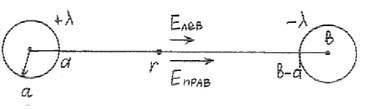
Тогда разность потенциалов или напряжение между проводами

U = b a∫−a E r dr( ) = 2πελ 0 b a∫−a  1r + b −1 r dr = 2πελ 0 ln b −aa −ln(b−r)r ar b a= −=                       = πελ0 ln b −aa  .

Ток вблизи левого проводника практически не зависит от заряда на правом

 (такой же ток втекает

во второй проводник), где 2πδa  площадь сечения пластины вокруг проводника, E a( ) = j_в .

пластине

Отсюда R .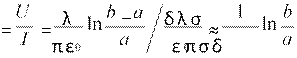

Ответ: .

                                                                                                                                          11

Неоднородный проводник:

8. В неоднородном цилиндрическом проводнике радиуса r₀ удельное сопротивление изменяется с расстоянием r от оси проводника по закону ρ ρ= ₀ rr₀ , где ρ₀ = const . По проводнику течет ток I₀ . Найти напряженность поля E внутри проводника, тепло выделяющееся на единицу длины проводника за время τ и сопротивление R_ед единицы длины проводника.

Решение:

 

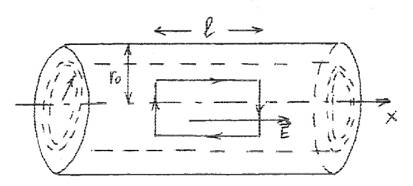
Выделим цилиндрический слой радиуса r и толщины dr с площадью dS = 2πrdr. По нему течет ток jdS EdS ( j = E  закон Ома в дифференциальной форме). Но "∫ Edl^{! !} = 0 или E r l( )₁ − E r l( )₂ = 0, т.е. внутри проводника E = const .

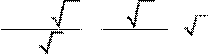
Тогда I0 = ∫r00 jdS = Er∫00 2πρrdr r0 r 0 = 2πρ0r E0 r∫00                    rdr ,            т.е.      I0 = 43πρr002 E                        или

Eвнутрипроводн. = 34ρπ0rI₀20 = const .

При I = const в цилиндрическом слое 2πrdr за время τ по закону Джоуля Ленца выделяется тепло dQ = ( )dI ² R_слояτ,

где ток в слое dI 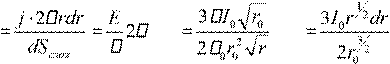rdr     rdr       ,

сопротивление слоя R_слоя = ^ρ_2π^l_rdr .

dQ 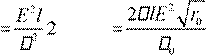π τrdr  rdrτ;

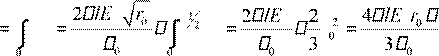         r₀                                              2               r₀                                                       2                                      2    2

Q       dQ                           r dr                      r                      .

Подставляя        l =1        и     E = 34ρπ0rI020 ,    находим       Qдлиныед.          = I042π3ρr002τ            и

U_еддлины_. =       −   = l=1Edx = I04⋅_π3ρr₀02 ⋅1.

                                 Uед.                3ρ

Тогда Rеддлины. = длиныI₀    = 4πr002 .

Ответ: Eвнутрипроводн. = 4πr0 = const , Qдлиныед. = I042π3ρr002τ , Rеддлины.    = UдлиныедI0.                                                                                = 43πρr002 .

9. Однородный цилиндрический проводник сделан из материала, удельное сопротивление которого меняется со временем по закону ρ ρ= _{0 }_τt _² , где ρ, τ  постоянные. По какому степенному закону в

_

зависимости от времени изменяется ток, пропускаемый через проводник, если за любое произвольное время τ в проводнике выделяется столько же тепла, сколько и при пропускании постоянного тока   I₀ через цилиндрический проводник того же радиуса, но с постоянным удельным сопротивлением ρ₀ за то же время τ.