Законы постоянного тока. Основные определения и формулы. Электрический ток. Сила тока. Дифференциальная форма уравнения непрерывности, страница 4

Решение:

Проводник длиной l и сечением S имеет сопротивление R = ρ_S^l .

Постоянный

ток

I0

выделяет

в

нем

тепло

Q = I R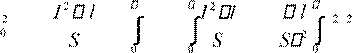τ= ^{0         0} τ= dQ =      dt =    ⁰                                                   I t dt ,

т. 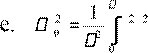      I     I t dt , где I = ktⁿ       степенной закон изменения тока со временем.

.

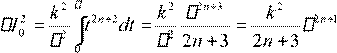Для произвольного времени τ 2n + =1 1 (степень τ слева и справа должна быть одинакова),  и искомый ток по-прежнему постоянен

k =3I₀ , I =       3I₀ .

Ответ: I =    3I₀ .

Переходные процессы:

10. Постоянная времени разряда плоского конденсатора, заполненного маслом с диэлектрической проницаемостью ε, через некоторое сопротивление была равна τ₀ . После того, как масло в конденсаторе отсырело, постоянная времени разряда через то же сопротивление уменьшилась в два раза. Определить удельное сопротивление ρ отсыревшего масла (ε не изменилось).

Решение:

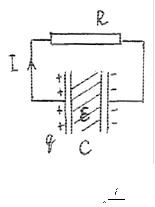Вначале диэлектрик идеален и закон Ома для цепи:

                                             RI =U_c = C^q , где I = − ^dq_dt (q       заряд на конденсаторе                                                      

убывает), т.е. − dqdt = RCq или q∫q0 dqq = − RC1 ∫0t dt ⇒ ln qq0 = − RCt

или q = q e₀  ^RC .

Постоянная разряда   это время, в течение которого напряжение (или заряд) конденсатора уменьшается в e раз, т.е. τ = RC .

Когда масло отсырело, то появится ток через него, т.е. внутренность конденсатора представит из себя проводник с сопротивлением R_c = ρ^d_S , где d  расстояние между пластинами, S  площадь пластин. Т.к. C = εεd0S , то Rc = ρεεC0 .

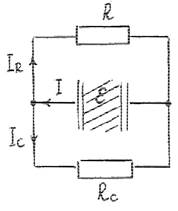                                                 I = I_R + I_C            



I = − dq           qt  _

                                                 I R_R − I R_{C C} = 0^

I RR = I RC C =UC = Cq , IR = RCq =τq0 . Решая систему, получим 

IC = IR RRC = IR ρRCεε0 = IR ρτεε0 0 = ρεεq 0 .

 1 + 1  = − dq или ∫q0 dqq = −∫0t dt ρεε τ1 0 + 10  .

Тогда I = IR + IC = q ρεε τ0 0       dt            q



ln qq0 = − ρεε τ1 0 + 10 t ; q = q e0 −ρεε τ1 0 + 10 t .

По условию ρεε τ τ τ1 + 1 = 1 = 12 = τ20 , т.е. ρεε τ0 = 0 , ρ= εετ00 .

                                        0           0            k           0

Ответ: ρ₌ ^τ0 . εε₀

11. Цепь состоит из источника постоянной э.д.с. ε и последовательно подключенных к нему сопротивления R и конденсатора C . Внутреннее сопротивление источника отсутствует. В момент         t = 0 емкость конденсатора скачком уменьшилась в n раз. Сколько тепла выделится на сопротивлении R за время τ?

Решение:

 

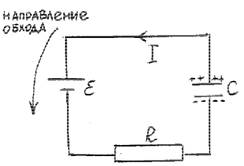
До момента t = 0 конденсатор был заряжен до предела ( )q₀ , ε=U_C0 = ^q_C⁰ и ток в нем не тек. При

изменении емкости U_C = _{C n}^q0 >ε и ток I потечет против направления ε (конденсатор начнет разряжаться).

2-е правило Кирхгофа: IR =U_C −ε= ^qn_C −ε (1).

Но ток I = − ^dq_dt (заряд на конденсаторе убывает), т.е. ^dq_dt = ^ε_R − _CR^qn (2), решив данное уравнение можно найти q t( ) и I _{= −} ^{dq t}_dt^{( )}.

Но поступим по-другому  продифференцируем уравнение (1) по времени:

R ^dIdt = CR dt^{n dq} = − CR^In , ^dI_dt = −_CR^In (это уравнение проще решать).

I^∫I0 dII = − CRn ∫₀t dt или ln II0 = − CRtn , I = I e0 −CRtn .

Начальный ток определяем из (2): I₀ = − ^dqdt _t=₀ ^{q n}CR⁰ − ^εR = (n −1₎^εR , _^{ q}_C⁰ =_ε^_,

^{ε −RC}nt .

т.е. I = (n −1)_R e

Тогда по закону Джоуля - Ленца за время τ выделится тепло

Q = τ∫0 I Rdt2 = n −1R)2 ε2 τ∫0 e−RCnt dt = − (n −1Rn)2 ε2RC e−RCnt τ0 = (n −1n)2 ε2C 1−e−RCnτ  . (

При τ→ ∞ Q ₌ ⁽ⁿ⁻¹_n^{)2 ε2C} . Можно показать, что это разность энергий

конденсаторов  2qC02 − 2qC n0′2           .

Ответ: Q = (n−1n)2 ε2C 1−e−RCnτ  .