Законы постоянного тока. Основные определения и формулы. Электрический ток. Сила тока. Дифференциальная форма уравнения непрерывности, страница 2

Решение:

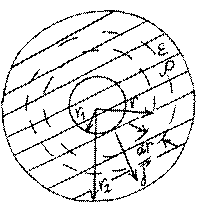Выделяем сферический слой с поверхностью

S = 4πr² , перпендикулярно которому от обкладки к обкладке течет ток. Если толщина слоя dr , то его сопротивление dR = ρ^dr_S .

Полное сопротивление R = ∫rr21 dR = 4ρπ r∫r21 drr2 = 4ρπ r11 − r12  .

Но Cсферичконденсатора. = 4πεεr2 −0rrr11 2 , т.е. 41π r11 − r12  = εεC0 и R = ρεεC 0 .

Тогда ток «разрядки» конденсатора I ^{= U}_R = _ρ^UC_εε0 .

Постоянен заряд через любое сферическое «сечение», т.к. внутри однородной среды не может накапливаться избыточный заряд. Т.е., плотность тока j r( ) = _4π^I_r2 = _{4π ρεεr}^UC₂ 0 =σE r( ) = _ρ¹ E = j  закон Ома в дифференциальной форме, т.е. E r( ) = _4πεε^UC0_r2  не зависит от ρ.

Ответ: R = ρεεC 0 , E r( ) = 4πεεUC0r2 .

5.  К центрам противоположных торцов тонкостенной цилиндрической банки диаметром D и высотой l припаяны провода диаметром d . Определить сопротивление банки R , если она сделана из жести толщиной δ$ d с удельной проводимостью σ.

Решение:

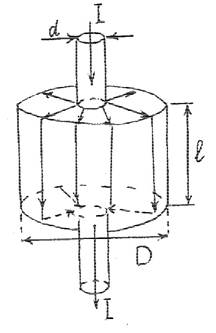
Ток I последовательно течет по верхнему основанию банки, по ее боковой поверхности и по нижнему основанию, т.е. R = R_осн. + R_бок. + R_осн.

поверх.

(последовательное соединение).

Боковая поверхность имеет сечение S =π δD⋅ , длину l и удельное сопротивление .е.

                                                        Rбокповерх. . = ρSl = σπ δlD         .

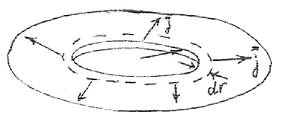
Основание разбиваем на маленькие кольца радиуса r и толщиной dr высотой δ.

Ток течет перпендикулярно боковой поверхности этих колец 2πδr , т.е. сопротивление кольца dR_к = ^ρ_2πδ^dr_r и D 2        D 2 сопротивление основания R_осн 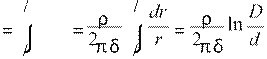         dR_к  .

                                                                                d 2                                d 2

В сумме Rбанки = σπlDS +2⋅ 2πδρ ln Dd = σπδ1  Dl +ln Dd  .

Ответ: Rбанки = σπδ1  Dl +ln Dd .

6. Заземление концов телеграфной линии осуществлено посредством металлических шаров радиусами r₁ и r₂ , очень глубоко зарытых в землю. Удельная проводимость почвы вблизи них равна σ₁ и σ₂ . Найти сопротивление R земли между шарами. Считать почву в окрестности каждого шара однородной на расстояниях, больших по сравнению с радиусами шаров.

Решение 1:

 

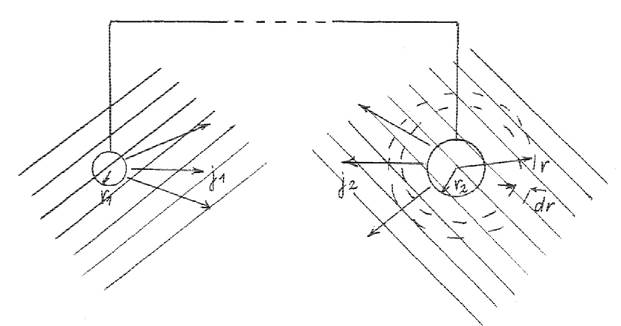
В силу однородности почвы ток будет течь от шара перпендикулярно его поверхности. Окружив шар слоем с площадью 4πr² и толщиной dr .

Определяем сопротивление слоя как dR_i = ρ_{i 4π σ π}^dR_r2 ^{= 1}i ₄^dr_r2 .

Т.е. сопротивление однородной почвы, заключающей большой объем вокруг каждого шара равно 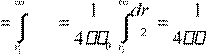R_i dR_{i r} i i_r .

Но сопротивление почвы вокруг обоих шаров складывается последовательно: R = R1 + R2 = 41π σ σ 11 1r + 12 2r .

Решение 2:

Поместим мысленно на левый шар заряд q₁, а на правый  q₂ . Тогда ток, стекающий с левого шара I₁ = 4πr j_{1 1}² = 4π σr₁² _{1 1}E  из закона Ома в дифференциальной форме.

Но E₁ ⁼ _4πεε^q0¹1 1_r2  поле вблизи заряженного шара, т.е. I₁ ⁼ _εε^q0¹1σ₁.

На второй шар точно такой же шар должен стекать из почвы:

I2 = qεε20σ22 = −I1 = −εεq1 10σ1 , т.е. q2 = − qσε1 1σε2 12 , где ε1 и ε2  диэлектрическая проницаемость почвы вблизи шаров, она может быть различной.

Потенциалы шаров: ϕ1 = Cqлев1.  = 4πεεq01 1 1r , ϕ2 = Cqправ2 . = 4πεεq02 2 2r = − 4πεσ εq01 1σ2 2r 1 .

                                                                 шара                                                      шара

Но из закона Ома I = I₁ = U^шарамимежду_R =ϕ ϕ1 −_R 2 , т.е.

R = ϕ ϕ1 −I 2 = 4 q1  1 + σσ εε12         q1 10σ1 = 41π σ σ 11 1r + 12 2r , результат не зависит от

                1              πεε0 1  r1    r2

диэлектрической проницаемости среды.

Ответ: R = 41π σ σ 11 1r + 12 2r  .