Расчет и программирование задачи о всестороннем растяжении пластинки с круговым отверстием, подкреплённым несимметричной оболочкой, страница 5

ur45:=gamma1*C[2]*Ii[1];

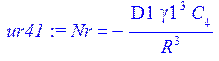
>h:=h0;R:=R0;T:=1/E;N:=nu/E;

E:=2*10^6;nu:=0.3;p:=1;

gamma1:=Pi*h:#узнать чему равна гамма

D1:=E*h^3/12*(1-nu^2):#узнать чему равна Д

> 

>otv:=solve({ur41,ur42,ur43,ur44,ur45},[Nr,C[1],C[2],C[3],C[4]]);

> 

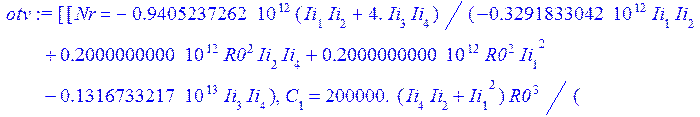
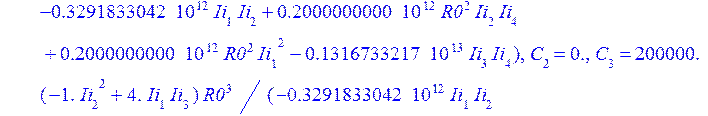
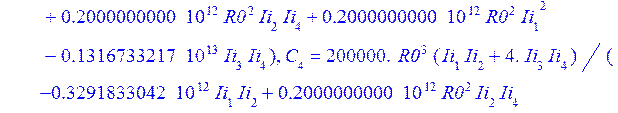
>Nr:=rhs(otv[1][1]):

C[1]:=rhs(otv[1][2]):

C[2]:=rhs(otv[1][3]):

C[3]:=rhs(otv[1][4]):

C[4]:=rhs(otv[1][5]):

> 

>Ii[1]:=(exp(beta*x)+exp(-beta*x))/2*cos(beta*x);

Ii[2]:=1/(2*beta)*((exp(beta*x)+exp(-beta*x))/2*sin(beta*x)+(exp(beta*x)-exp(-beta*x))/2*cos(beta*x));

Ii[3]:=1/(2*beta^2)*((exp(beta*x)-exp(-beta*x))/2*sin(beta*x));

Ii[4]:=1/(4*beta^4)*((exp(beta*x)+exp(-beta*x))/2*sin(beta*x)-(exp(beta*x)-exp(-beta*x))/2*cos(beta*x));

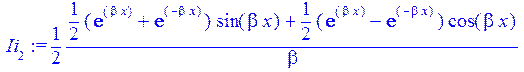
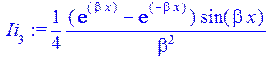
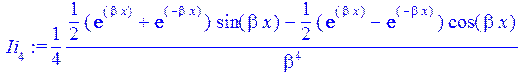
>W:=sum(C[i]*Ii[i],i=1..4);#функция прогиба

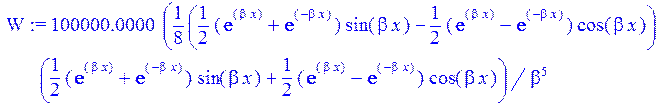
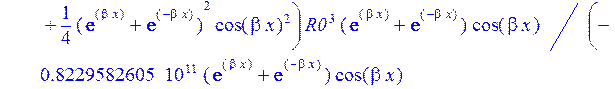
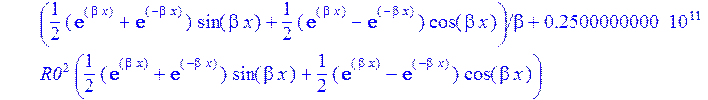
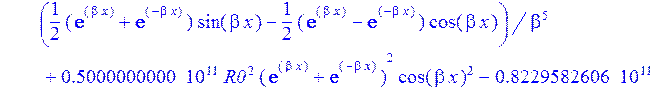
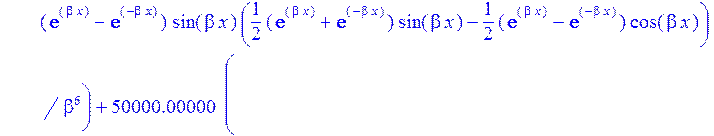
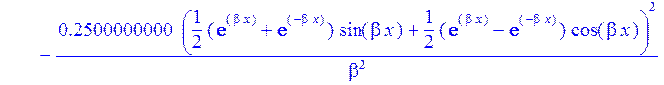
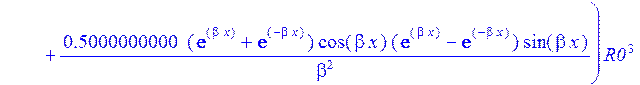
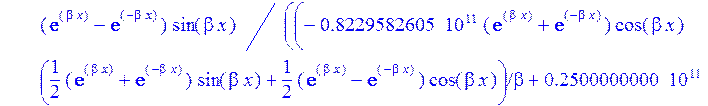
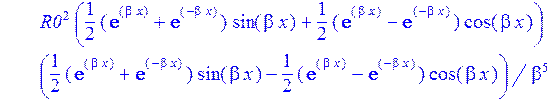
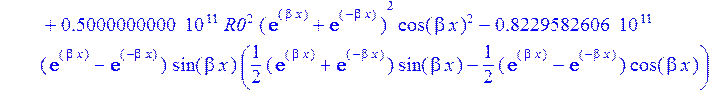
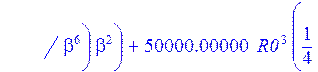
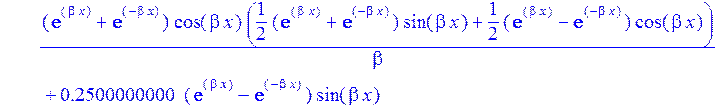
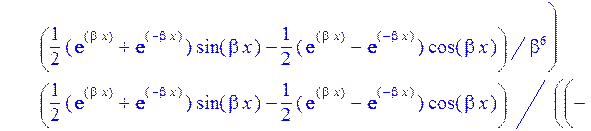
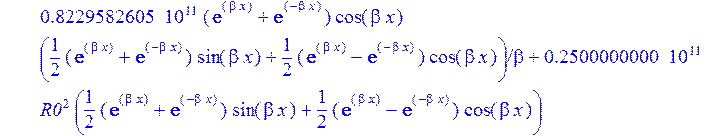
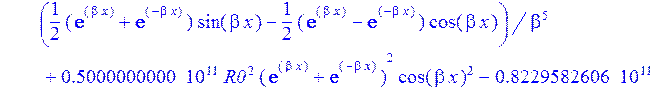
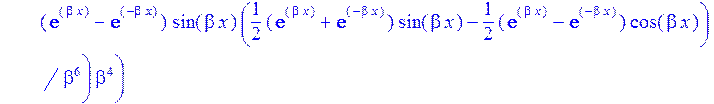
>sigma:=2*p-Nr/h:#Тангенсальные напряжения в пластинке на контуре Г

>sigma1:=E/(R*h0)*(C[1]*Ii[1]+C[3]*Ii[3]+C[4]*Ii[4]):# Тангенсальное напряжение в оболочке от растяжения

>sigma2:=6*D1*gamma1^2*nu/h0*(-4*C[1]*Ii[3]+C[3]*Ii[3]+C[4]*Ii[2]):# Тангенсальное напряжение в оболочке от сжатия

>plot3d(subs(R0=5,W),beta=0..2,x=0..2);#Функция прогиба

> 

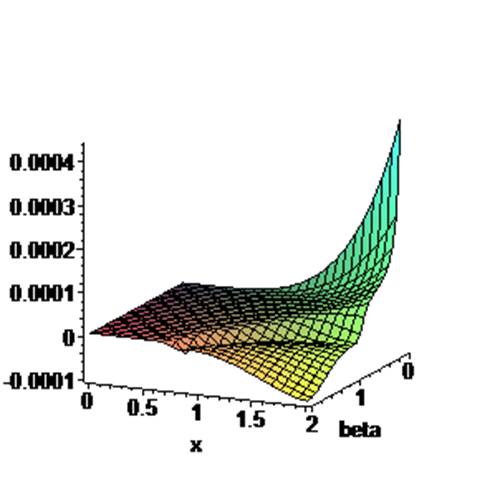
>beta:=4:x:=2:

>plot(sigma,R0=0..10);#

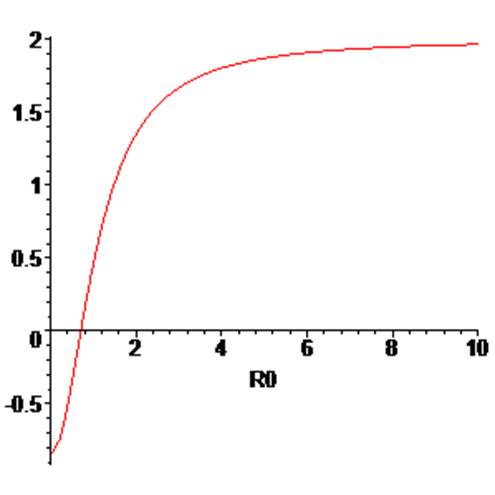
>plot(sigma1,R0=0..10);

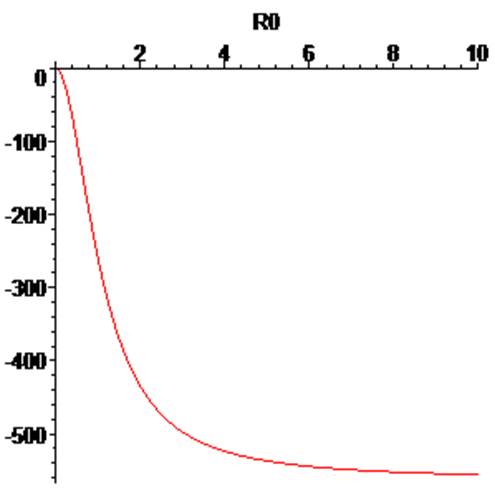
>plot(sigma2,R0=0..10);

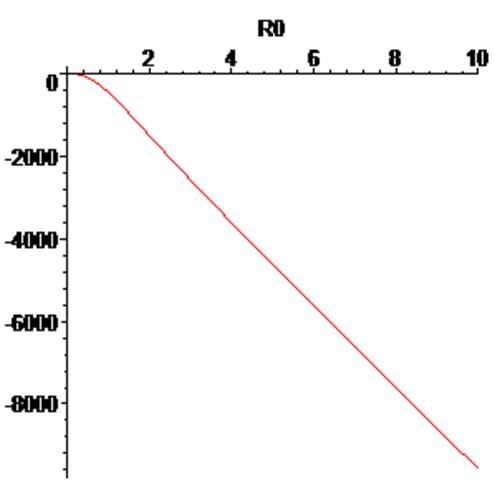
3.2. Числовые результаты

Для конкретного случая подкрепления пластично симметричной оболочкой на рис. 6приведена эпюра напряжения  и  по высоте оболочки.

Во многих работах считалось, что постоянны по высоте подкрепляющего кольца. Однако, даже для таких колец, у которых наблюдаются отклонения эпюры  от равномерного закона в точках .

Аналогичные результаты можно получить при подкреплении пластинки односторонней оболочкой. В этом случае необходимо приписывать появление изгибающего момента в области контакта между пластинкой и оболочкой.

На рис. 7 приведены эпюры тангенциальных напряжений  и  по высоте оболочки для случаев расчёта с учётом и без учёта изгиба пластинки, а на рис.8  приведены эпюры суммарных напряжений в оболочке для этих случаев.

Можно отметить, что учет изгибающего момента не оказывает существенного влияния на напряженное состояние в оболочке и значительно  сказывается на состоянии пластинки.

Глава 4. Графическое решение

4.1 Графическое исполнение

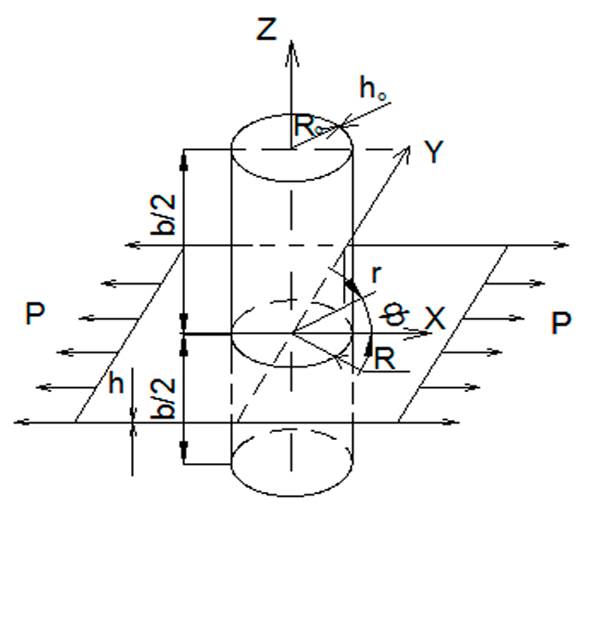
Рис 1. Схема подкрепления пластинки симметричной оболочкой.

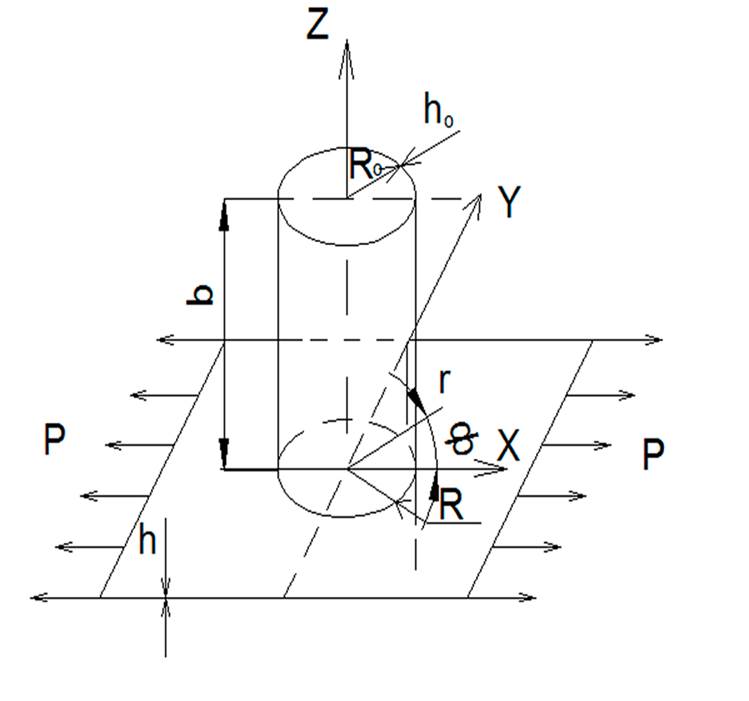
Рис 2. Схема подкрепления пластинки односторонней оболочкой.

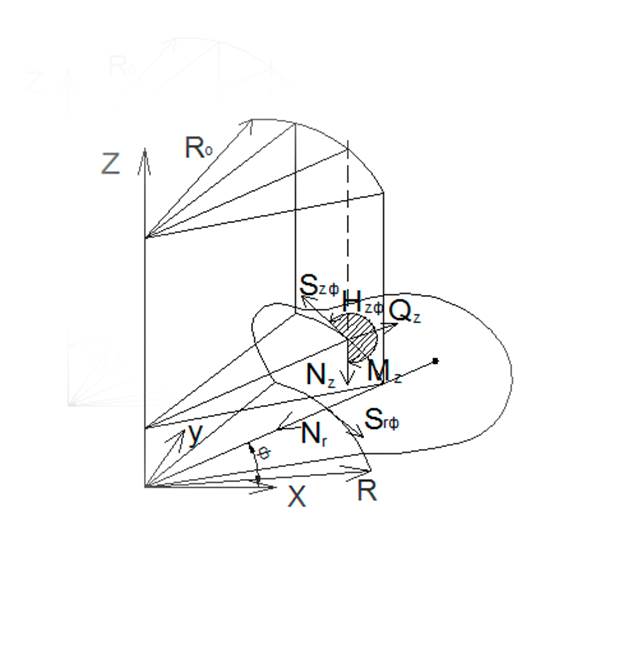
Рис 3. Усилия в области контакта при подкреплении пластинки симметричной оболочкой

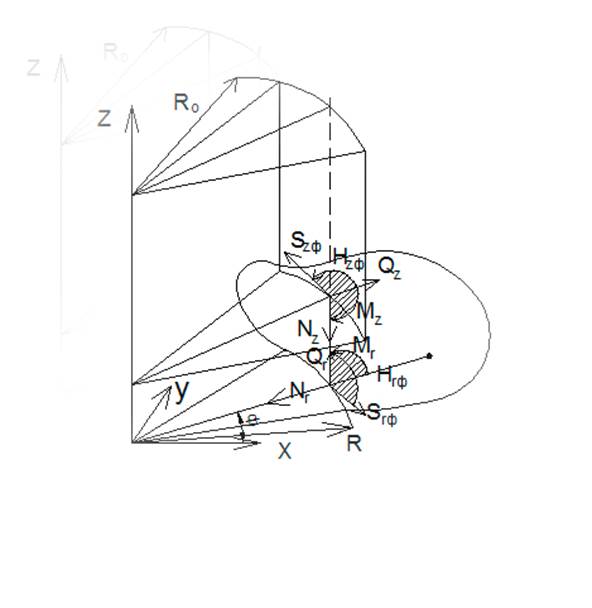
Рис 4. Усилия в области контакта при подкреплении пластинки односторонней оболочкой

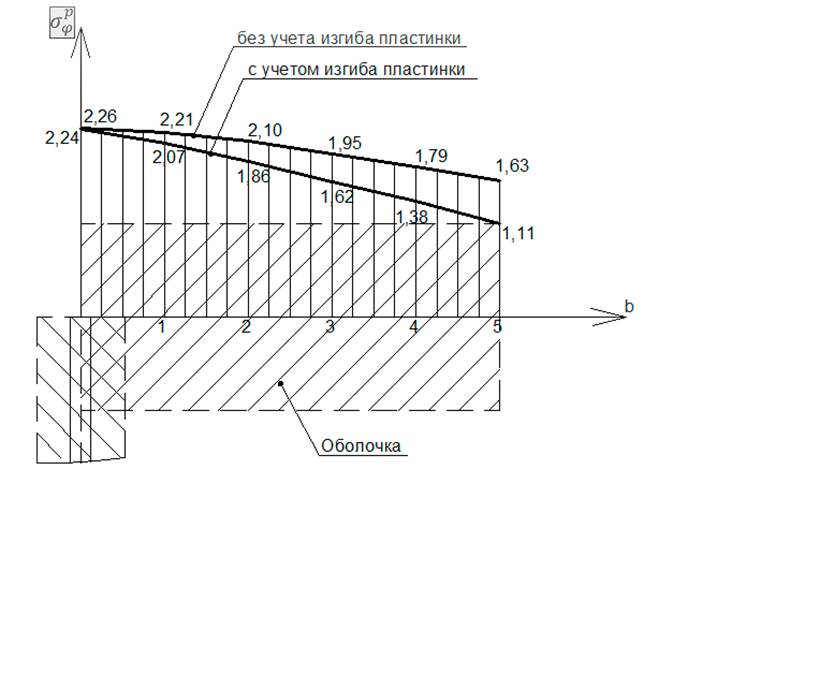
Рис 5. Эпюра изгиба по высоте оболочки с учётом изгиба пластинки.

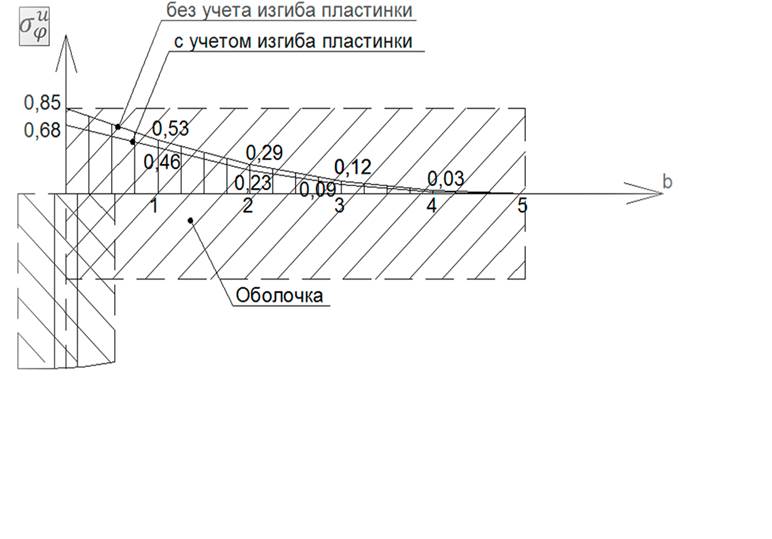
Рис 6. Эпюра изгиба по высоте оболочки без учёта изгиба пластинки.

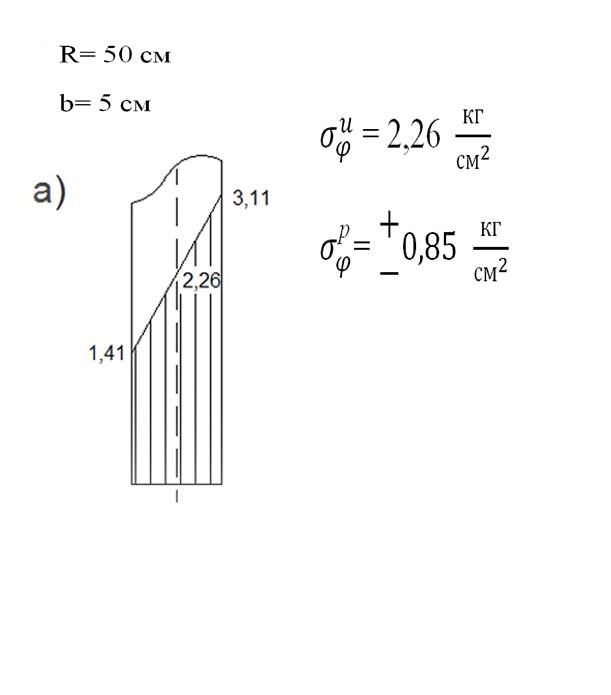
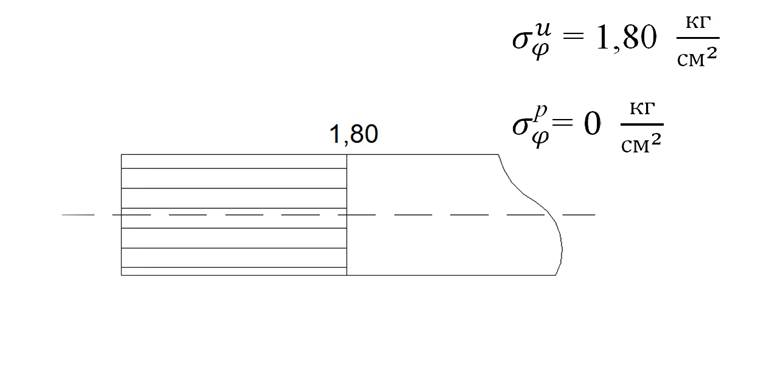
Рис 7. Эпюры суммарных напряжений в оболочке в сечении и пластинки в сечении без учёта изгиба пластинки.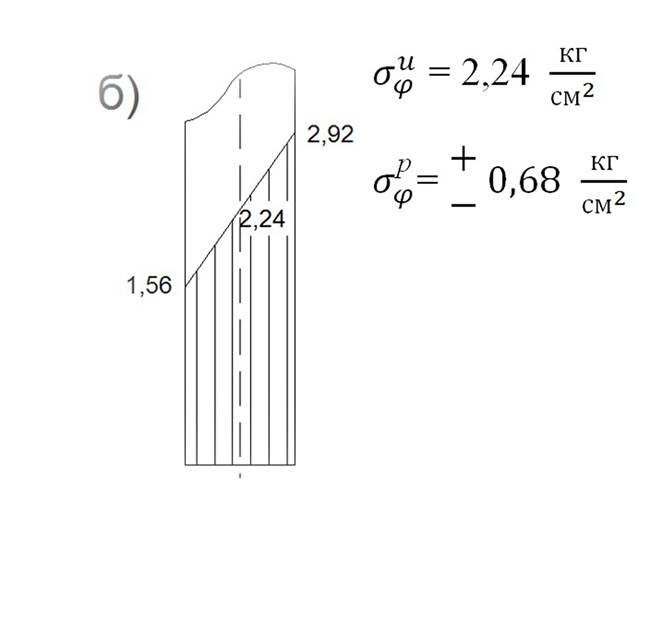

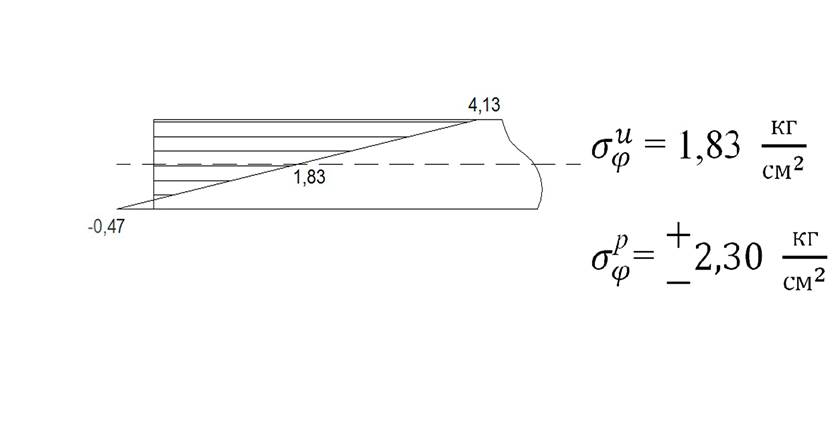
Рис 8. Эпюры суммарных напряжений в оболочке в сечении и пластинки в сечении с учётом изгиба пластинки.

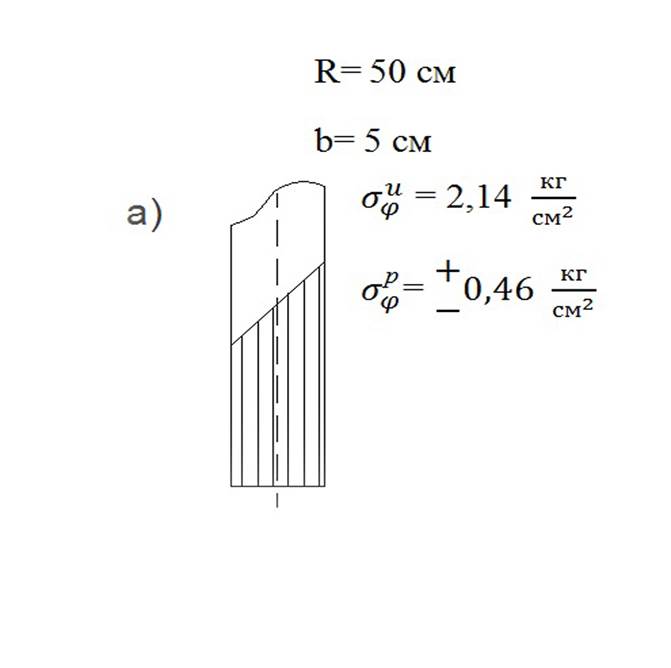
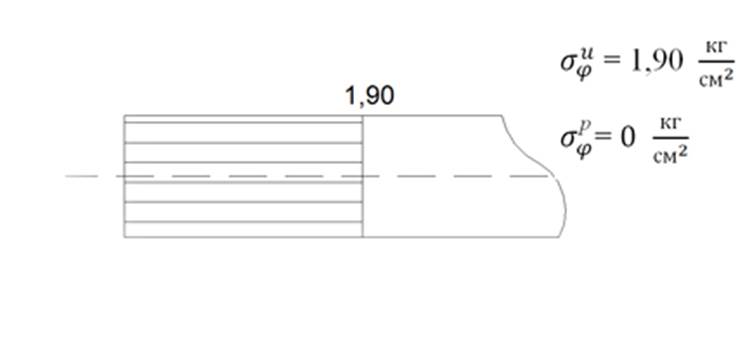
Рис 8. Эпюры суммарных напряжений в оболочке в сечении  Ɛ=0 и пластинки в сечении R без учёта изгиба пластинки для случаев R=50, b=5,

.

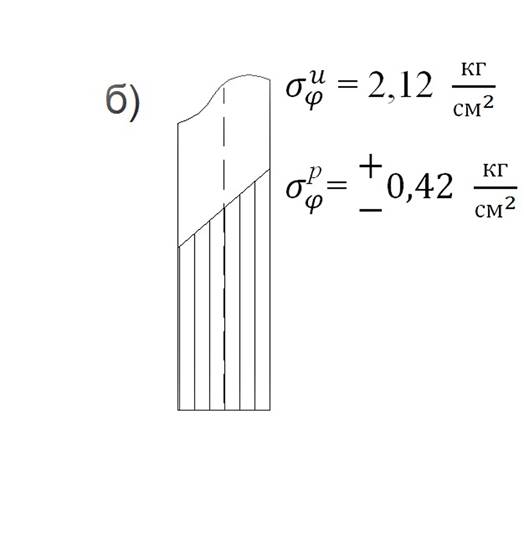
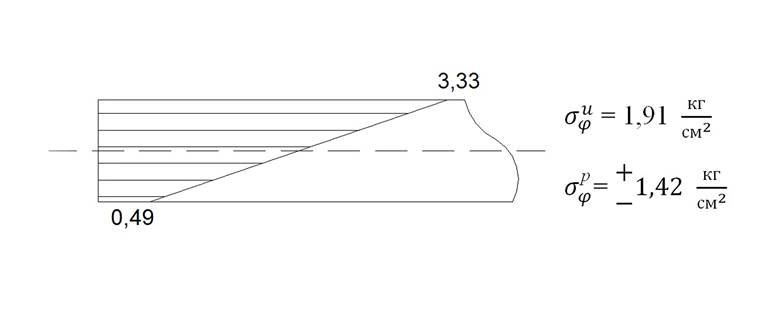
Рис 8. Эпюры суммарных напряжений в оболочке в сечении  Ɛ=0 и пластинки в сечении R с учётом изгиба пластинки для случаев R=50, b=5,

.

Заключение.

Таким образом, в настоящей работе получено решение ряда задач об упругом сопряжении пластин и оболочек.

Полученные условия упругого сопряжения пластинки с круговым вырезом и тонкой, круговой цилиндрической оболочкой, расположенной или симметрично, или только с одной стороны.

В случае одностороннего расположения оболочки необходимо учитывать о появлении изгибающего момента в области контакта между пластинкой и оболочкой.