Для решения поставленной задачи введём две системы координат : 1 – полярную (r,ᵠ) – для пластинки с началом координат в центре круга; 2-цилинрическую (r,ᵠ,z)для оболочки (рис 2).
1.2 Условия упругого сопряжения
Условия упругого сопряжения в области контакта пластинки с оболочкой понимаются так, что главный вектор и главный момент сил взаимодействия пластинки равны главному вектору и главному моменту оболочки , а векторы упругого перемещения и поворота пластинки равны соответствующим векторам перемещения и поворота оболочки [3].
Обозначим контур сопряжения через Г. Тогда на Г имеем следующие условия сопряжения:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
Где обозначено для пластинки:
![]() +
+![]() +
+![]() (2.5)
(2.5)
![]() +
+![]() (2.6)
(2.6)
![]() +
+![]() +W
+W![]() (2.7)
(2.7)
![]() +
+![]() (2.8)
(2.8)
И для оболочки:
![]() +
+![]() +
+![]() (2.9)
(2.9)
![]() +
+![]() (2.10)
(2.10)
![]() +
+![]() +
+![]() (2.11)
(2.11)
![]() +
+![]() (2.12)
(2.12)
В выражениях (2.5-2.8) и
(2.9 - 2.12) приведено разложение векторных величин ![]() ,
,![]() ,
,![]() ,
,
![]() на
оси подвижного релера кривой Г (
на
оси подвижного релера кривой Г (![]() ).
).
Переходя в выражениях (2.1-2.4) от векторных величин к их проекциям на соответствующие оси по (2.5 - 2.8) и (2.9 - 2.12) получим:
Для симметричного расположения оболочки:
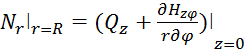 (2.13)
(2.13)
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
Для одностороннего расположения оболочки
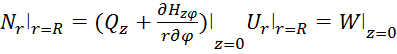 (2.17)
(2.17)
![]() (2.18)
(2.18)
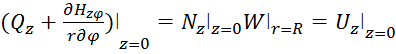 (2.19)
(2.19)
![]() (2.20)
(2.20)
В данном случае для полярно-симметричной задачи вместо (2.13 – 2.16) и (2.17 – 2.20) получим соответственно
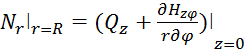 (2.21)
(2.21)
![]() (2.22)
(2.22)
и
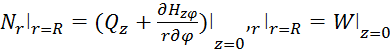 (2.23)
(2.23)
![]() (2.24)
(2.24)
Кроме условий (2.21 – 2.22) или (2.23 – 2.24) необходимо задать однородные силовые условия на свободном конце оболочки, а так же учесть нагрузку на «бесконечности» для пластинки.
Глава 2. Методы решения задачи
2.1 Метод решения задачи
Для решения задачи
отделим пластинку от оболочки и рассмотрим задачу об определении напряженного
состояния пластинки под действием усилий на бесконечности и реактивных усилий ![]() и
момента
и
момента ![]() .
Считаем, что в силу линейности задачи компоненты напряженного состояния от
растяжения и изгиба могут быть определены независимо друг от друга.
.
Считаем, что в силу линейности задачи компоненты напряженного состояния от
растяжения и изгиба могут быть определены независимо друг от друга.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.