Решая эти две задачи методами плоской задачи упругости [3] ,получим на контуре слоя Г :
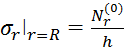 (3.1)
(3.1)
 (3.2)
(3.2)
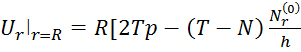 ]
(3.3)
]
(3.3)
Где T=![]() N=
N=![]()
А так же
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
Далее рассмотрим осе
симметрическое напряженное состояние цилиндрической оболочки, загруженной в
сечении z=0
реактивными усилиями ![]() и
моментом
и
моментом ![]() .
.
Для решения задачи используем дифференциальное уравнение осе симметричной деформации оболочек в виде [2]
![]() +4
+4![]() (3.8)
(3.8)
Где
![]() -
функция прогиба
-
функция прогиба
![]() –
вертикальная координата =
–
вертикальная координата =![]()
4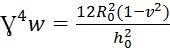
![]() –
толщина оболочки
–
толщина оболочки
![]() -
её радиус
-
её радиус
Решение (3.8) представим в виде
![]() (γ𝝃)
(3.9)
(γ𝝃)
(3.9)
Где
![]() -
неизвестные коэффициенты
-
неизвестные коэффициенты
![]() (γ𝝃)
– функции А.Н.Крылова[3]
(γ𝝃)
– функции А.Н.Крылова[3]
Параметрами изгиба оболочки могут быть записаны в виде
![]() γ(-4
γ(-4![]() +
+![]() +
+![]() +
+![]() )
(3.10)
)
(3.10)
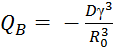 (-
4
(-
4![]() +
+![]() )
(3.11)
)
(3.11)
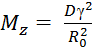 (-
4
(-
4![]() +
+![]() )
(3.12)
)
(3.12)
2.2 Пластинка, подкреплённая симметричной оболочкой
Для данного случая, используя (2.21 – 2.22) и однородные условия для оболочки, получим такие граничные условия:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
Кроме этого, необходимо считать в силу симметричности расположения оболочки что
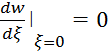 (4.5)
(4.5)
Подставляя в (4.1 - 4.4) и (4.5) выражения по (3.1 – 3.3) и (3.10 – 3.12)
, получим следующую систему пяти алгебраических уравнений
![]() (4.6)
(4.6)
2RTp-R(T-N)![]() =C
(4.7)
=C
(4.7)
-4![]() -4
-4![]() -4
-4![]() +4
+4![]() =0
(4.8)
=0
(4.8)
-4![]() -4
-4![]() +
+![]() +
+![]() =0
(4.9)
=0
(4.9)
γ![]() =0
(4.10)
=0
(4.10)
Относительно ![]() (j=1,….4)
и
(j=1,….4)
и ![]() .
.
При расчете принято, что
толщина пластинки ![]() ,
и радиус отверстия R равен радиусу оболочки
,
и радиус отверстия R равен радиусу оболочки ![]() .
.
В матричном виде уравнения (4.6 - 4.10) можно записать так
![]() =
=![]() *
*![]() (4.11)
(4.11)
j=1,2…4.
k=1,2…4.
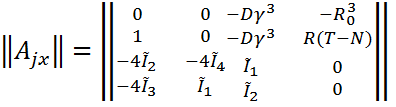 (4.12)
(4.12)
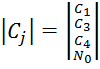 (4.13)
(4.13)
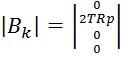 (4.14)
(4.14)
Здесь учтено, что ![]() .
.
Тангенциальные напряжения
![]() в
пластинке на контуре Г могут быть определены по формуле
в
пластинке на контуре Г могут быть определены по формуле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.