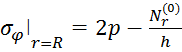 (4.15)
(4.15)
Тангенциальное напряжение в оболочке а) от растяжения
![]() =
=![]() (4.16)
(4.16)
б) от изгиба
![]() =+-
=+-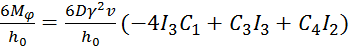 (4.17)
(4.17)
2.3 Пластинка, подкреплённая односторонней оболочкой
Граничные условия.
![]() (5.1)
(5.1)
![]() (5.2)
(5.2)
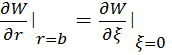 (5.3)
(5.3)
![]() (5.4)
(5.4)
![]() (5.5)
(5.5)
![]() (5.6)
(5.6)
![]() (5.7)
(5.7)
Подставляя в выражения
для ![]() и
и ![]() получим
следующую систему шести алгебраических уравнений в матричном виде:
получим
следующую систему шести алгебраических уравнений в матричном виде:
![]() =
=![]() *
*![]() (5.8)
(5.8)
j=1,2…6.
Где
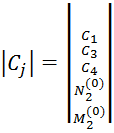 (5.9)
(5.9)
Относительно шести неизвестных
![]() (j=1,2,3,4)
,
(j=1,2,3,4)
,![]() ,
,![]() .
.
Приведём матрицу этой
системы и вектор столбец свободных членов ![]() .
.
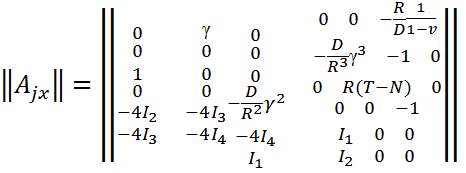 (5.10)
(5.10)
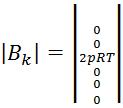 (5.11)
(5.11)
Напряжения в пластинке могут быть определены по формулам а) растяжения
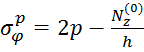 (5.12)
(5.12)
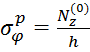 (5.13)
(5.13)
![]() (5.14)
(5.14)
б) изгиба
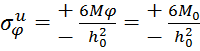 (5.15)
(5.15)
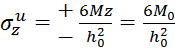 (5.16)
(5.16)
![]() (5.17)
(5.17)
Напряжения в оболочке могут быть определены по формулам а) растяжения
![]() =0
(5.18)
=0
(5.18)
![]() (5.19)
(5.19)
![]() =
=![]() .
(5.20)
.
(5.20)
б) изгиба
![]() =+-
=+-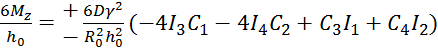 (5.21)
(5.21)
![]() (5.22)
(5.22)
![]() =+-
=+-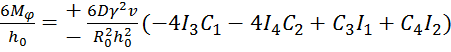 (5.23)
(5.23)
Глава 3. Програмирование задачи
3.1 Программирование задачи
Решение матричного уравнения (4.11) было запрограммировано в программе Maple.
Принять следующие исходные данные :
Модуль Юнга Е=2*![]() кг/
кг/![]()
Коэффициент Пуассона v=0,3
R=![]()
h=![]()
P=1
b=5,6,7,8,9.
>restart;
>#o:=z/R0;# вертикальная координата
#R0:=50;#радиус оболочки
h0:=1;#толщина оболочки
Ii:=array(1..4):
![]()
>ur41:=Nr=-(D1*gamma1^3)/R^3*C[4];
ur42:=2*R*T*p-R*(T-N)*Nr=C[1];
ur43:=-4*Ii[2]*C[1]-4*Ii[3]*C[2]-4*Ii[4]*C[3]+4*Ii[1]*C[4]=0;
ur44:=-4*Ii[3]*C[1]-4*Ii[4]*C[2]+Ii[1]*C[3]+Ii[2]*C[4]=0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.