Экспериментальное исследование численных методов решения систем линейных алгебраических уравнений

Санкт-Петербургский Государственный

Политехнический Университет

Отчет о лабораторной работе № 1.

«ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ  ЧИСЛЕННЫХ  МЕТОДОВ  РЕШЕНИЯ  СИСТЕМ ЛИНЕЙНЫХ  АЛГЕБРАИЧЕСКИХ  УРАВНЕНИЙ»

                                                                                                                                   Выполнил:

                                                                                                                студент группы 2091/1

                                                                                                                         Журавлев Иван

                                                                                                                                       Преподаватель

Анисимов Андрей

Санкт-Петербург

2005 г.

1 Сравнение естественного и стандартного числа обусловленности матрицы

После проведения ряда численных экспериментов была составлена следующая таблица:

порядок матрицы	номер тестовой  матрицы	естественное число µ1	стандартное число µ2	оценка стандартного числа cond
5	1	1,5E+02	1,6E+02	5,7E+01
6	2	6,1E+01	8,4E+01	7,1E+01
5	6	4,8E+09	1,2E+10	1,4E+10
6	2	6,1E+01	8,4E+01	7,7E+01
7	4	1,8E+01	6,8E+01	3,0E+01
8	6	1,5E+15	7,8E+18	8,4E+18
15	6	3,9E+11	1,5E+14	7,2E+14

Вывод: Проанализировав ее,  можно сделать некоторые предварительные выводы:

 Относительное различие стандартного и естественного числа обусловленности  невелико—всегда в пределах одного порядка. Чем хуже обусловлена матрица(чем выше µ1 иµ2) тем меньше они отличаются. Для матриц с хорошей обусловленностью точность оценки стандартного числа с помощью процедуры DECOMP  зависит от того, каким алгоритмом генерировалась матрица. Например, µ2 матрицы, сгенерированных по алгоритму 2 оценивались достаточно точно. А для матриц, сгенерированных по алгоритму1 оценка cond отличалась от µ2 иногда даже на один порядок.  Естественно, что  на практике стараются сводить поставленные задачи к системам с хорошо обусловленными  матрицами (). Так как в этом случае чувствительность решения к погрешности исходных данных мала. Если же невозможно обойти использование плохо обусловленной матрицы, то необходимо обеспечить высокую точность исходных данных, в противном случае мы рискуем получить  результаты, не  имеющие к действительности никакого отношения.

2 Исследование точности решения как функции от порядка матрицы при постоянном числе обусловленности(хорошо обусловленные матрицы)

После проведения многочисленных испытаний была получена масса материала. Однако  в ходе анализа были оставлены как наиболее показательные следующие данные:

порядок матрицы	номер тестовой  матрицы	естественное число µ1	стандартное число µ2	фактическая ошибка	оценка  ошибки
6	2	6,10E+01	8,4E+01	0	0
7	4	1,80E+01	6,8E+01	2,10E-12	4,30E-11
13	4	5,20E+01	1,8E+02	1,20E-11	2,60E-10

Из таблицы видно, что при практически постоянном числе  обусловленности ошибка  возрастает при возрастании порядка.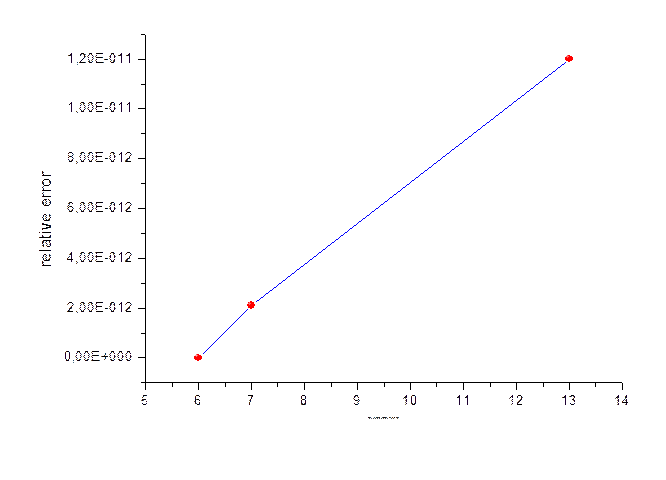

Вывод: Такой  характер зависимости можно объяснить тем, что в методе Гаусса при возрастании порядка системы возрастает число операций сложения и деления и, как следствие,  число округлений. 

3 Исследование точности решения как функции от порядка матрицы при постоянном числе обусловленности (плохо обусловленные матрицы).

Были проведены аналогичные Пункту№2 исследования и получены следующие результаты:

порядок матрицы	номер тестовой  матрицы	естественное число µ1	стандартное число µ2	фактическая ошибка	оценка  ошибки
9	12	6,40E+14	1,5E+16	7,2E+00	6,80E+03
10	11	4,80E+13	7,9E+14	1,0E+01	1,60E+02
12	12	3,00E+14	1,7E+17	1,2E+02	2,50E+05

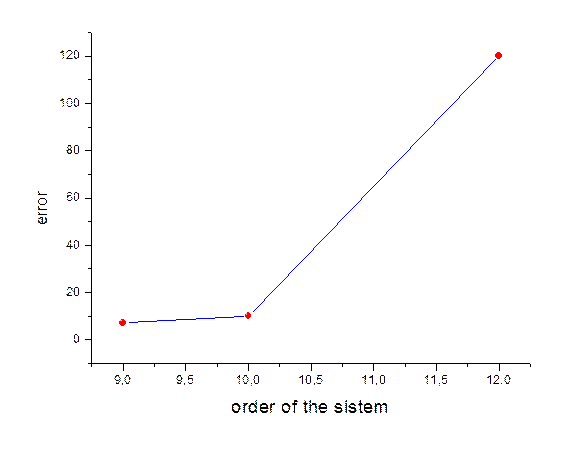
Вывод: Нетрудно заметить, что возрастание относительной погрешности при росте порядка системы имеет более быстрый характер. Что, собственно, и предсказывается теорией.

Необходимо отметить, что оценка погрешности с помощью процедуры DECOMP дает сильно завышенное значение. Конечно же, в случае плохо обусловленных матриц применение данных алгоритмов решения нецелесообразно, так как погрешность достигает положительных степеней. То есть необходимо использовать какие-то иные алгоритмы. Какие?

4  Исследование зависимости точности решения от числа обусловленности при постоянном порядке системы.

Были проведены эксперименты с матрицей порядка 7.

Результаты измерений могут быть представлены следующими таблицей и графиками. График зависимости ошибки от обусловленности?

µ1	µ2	фактическая ошибка	величина нормы вектора невязки ||r||
2,30E+01	3,10E+01	1,20E-11	1,50E-09
8,80E+07	3,60E+08	4,90E-07	4,60E-10
1,30E+08	2,30E+08	1,70E-05	1,90E-10
7,50E+08	1,30E+09	1,40E-04	2,70E-09
7,40E+15	1,10E+17	1,30E+01	1,50E-10

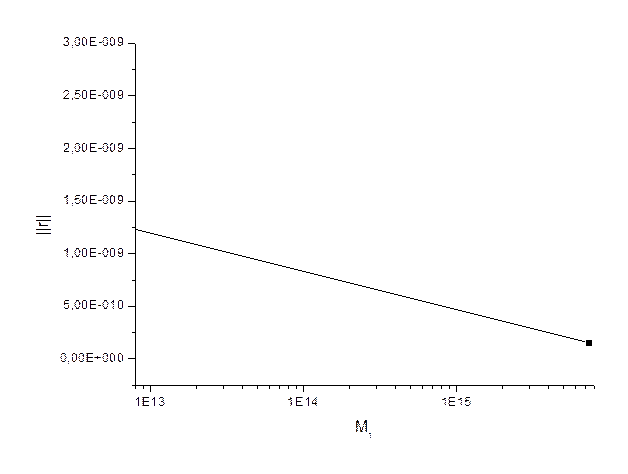
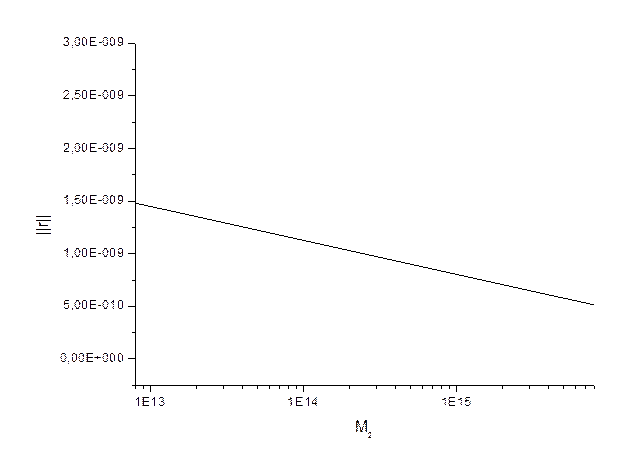
Вывод: Как и следовало ожидать, относительная ошибка возрастает с ростом числа обусловленности. При достаточно высоких числах обусловленности(порядка 10^15) использование алгоритма Гаусса становиться нецелесообразным, так как погрешность имеет уже положительные степени. Какую либо зависимость вектора невязки от числа обусловленности установить не удалось.Почему?

5.Исследование возможности улучшения обусловленности задачи путем внесения в матрицу малого случайного возмущения.