Численные методы решения обыкновенных дифференциальных уравнений

Министерство образования РФ

Санкт - Петербургский государственный политехнический университет

Радиофизический факультет

Кафедра радиофизики

по курсу ''Численные методы''

тема: ”Численные методы решения обыкновенных  дифференциальных уравнений”

                                                                      Преподаватель:Львов Б.В.

                                                                      Студент:Зайцев Р.А.

Группа: 2091/3

Санкт - Петербург

2003 г.

Работа выполняется при следующих начальных условиях:

Тестовые матрицы-1,3,5,6,7

Рабочие матрицы-23,25,27,33,38

Настоящая работа ставит целью сравнительный анализ вычислительных схем решения задачи Коши для обыкновенных дифференциальных уравнений (ОДУ). Такая задача формули­руется в следующем виде

                     

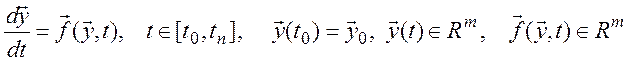
1. При интегрировании систем линейных уравнений на основе информации о значениях собственных чисел матрицы системы оценить максимальную величину шага устойчивого интегрирования и проверить эту оценку экспериментально.

Будем пользоваться несколькими задачами, с соответственно разными собственными числами, влияющими на сходимость данной задачи.

1а) ЯВНЫЙ  МЕТОД ЭЙЛЕРА.

Рассмотрим исследуемые нами задачи на предмет сходимости процесса на графике первой наблюдаемой компоненты вектора состояния.                                                                                      Для примера приведем графики процессов сходимости тестовых матриц №№№1,5,7:

Для тестовой матрицы №1 (первый график ,h=0.1) метод устойчив и сходится;

Для тестовой матрицы №5 (третий график ,h=1.0) поcле критического h метод начинает явно расходиться;

Для тестовой матрицы №7 (четвертый график ,h=1.1) метод расходится.

Матрица №1 l1=-1+j l2=-1-j		Матрица №3 l1=-7 l2=-1		Матрица №5 l1=j l2=-j		Матрица №7 l1=1+j l2=1-j
h	Результат	h	Результат	h	Результат	h	Результат
0.1	сходится	0.1	сходится	0.1	–	0.1	–
0.4	сходится	0.12	сходится	0.3	–	0.3	–
0.9	сходится	0.2	сходится	0.9	–	0.9	–
1.0	~	0.215	~	1.0	–	1.0	–
1.1	–	0.23	–	10.0	–	10.0	–

Значок ”~’’ означает,что метод сходится медленнее.

Значок ''-'' означает,что метод не сходится.

Вывод: В результате следует отметить, что  у матрицы№1 максимальная величина шага практически в 5 раз превышает тот же показатель для матрицы №2.Таким образом ясно, что в случае матрицы №1 метод сходится гораздо быстрее. Для систем №5,№7 метод расходится.

Справедливо соотношения |1+lh|<=1, (1+U)²+V²<=1

Этому неравенству удовлетворяют точки на комплексной плоскости lh, лежащие в единичной окружности с центром в точке(1,0). Для этих точек явный метод Эйлера абсолютно устойчив. Чем больше l, тем меньше должен быть выбран h.

1б)  НЕЯВНЫЙ МЕТОД ЭЙЛЕРА.

 Приведены графики сходимости метода для матриц №№1,7

Матрица №1 l1=-1+j l2=-1-j		Матрица №3 l1=-7 l2=-1		Матрица №5 l1=j l2=-j		Матрица №7 l1=1+j l2=1-j
h	Результат	h	Результат	h	Результат	h	Результат
0.1	сходится	0.1	сходится	0.1	сходится	0.1	сходится
0.5	сходится	0.5	сходится	0.5	сходится	0.5	сходится
1.0	сходится	1.0	сходится	1.0	сходится	1.0	сходится
5.0	сходится	5.0	сходится	5.0	сходится	5.0	сходится
10.0	сходится	10.0	сходится	10.0	сходится	10.0	сходится

Вывод: В результате следует отметить, что неявный метод Эйлера сходится везде вне зависимости от шага интегрирования. Справедливо соотношение |1-lh|>=1, , (1+U)²+V²>=1

Этому неравенству удовлетворяют точки на комплексной плоскости lh, лежащие вне единичной окружности с центром в точке(1,0). Для этих точек явный метод Эйлера абсолютно устойчив. При lh<0 неявный метод Эйлера сходится везде, независимо от величины шага интегрирования.

1в)  МЕТОД ТРАПЕЦИЙ ДЛЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Приведены графики сходимости метода для матриц №№№1,5,7.

Матрица №1 l1=-1+j l2=-1-j		Матрица  №3                     l1=-7 l2=-1		Матрица №5 l1=j l2=-j		Матрица №7 l1=1+j l2=1-j
h	Результат	h	Результат	h	Результат	h	Результат
0.1	сходится	0.1	сходится	0.1	~	0.1	–
0.5	сходится	0.5	сходится	0.5	~	0.5	–
1.0	сходится	1.0	сходится	1.0	~	1.0	–
5.0	сходится	5.0	сходится	5.0	~	5.0	–
10.0	сходится	10.0	сходится	10.0	~	10.0	–

Значок ”~’’ означает,что метод сходится медленнее.

Значок ''-'' означает,что метод не сходится.

Вывод:В результате следует отметить, что метод трапеций устойчив в том случае, когда вещественная часть корней отрицательна, иначе метод расходится независимо от шага интегрирования.

1г) МЕТОД РУНГЕ-КУТТЫ 2-ОГО ПОРЯДКА.

Формулы этих методов идеально приспособлены для практических расчетов: они позволяют легко менять шаг интегрирования, являются одношаговыми, достаточно экономичны, по крайней мере, до формул четвертого порядка включительно.

Графики приведены для тестовой матрицы №1   h=1.3; h=1.54 ; h=1.6