4.3. Аппроксимация функций алгебраическими полиномами
4.3.1. Равномерное приближение функций
Пусть
функция f(x) задана
таблицей своих значений ![]() . Без ограничения общности можно
считать, что
. Без ограничения общности можно
считать, что ![]() . Всякий
полином
. Всякий
полином 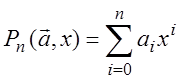 , порядок
которого
, порядок
которого ![]() , по отношению
к заданной таблице
, по отношению
к заданной таблице ![]() имеет
естественную характеристику близости – максимальное уклонение
имеет
естественную характеристику близости – максимальное уклонение
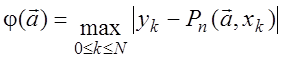 .
(4.23)
.
(4.23)
Пусть при фиксированном значении порядка полинома (n)
![]() .
(4.24)
.
(4.24)
Тогда полином ![]() , для которого выполняется
условие
, для которого выполняется
условие
![]() , (4.25)
, (4.25)
называется полиномом
наилучшего равномерного приближения таблицы ![]() .
.
Решение
задачи наилучшего приближения (построение полинома ![]() ) существенно зависит от
соотношения между значениями порядка полинома (n) и «длины» таблицы
(N). Так, если n=N, то задача
построения полинома наилучшего равномерного приближения трансформируется в
задачу классической интерполяции, для которой
) существенно зависит от
соотношения между значениями порядка полинома (n) и «длины» таблицы
(N). Так, если n=N, то задача
построения полинома наилучшего равномерного приближения трансформируется в
задачу классической интерполяции, для которой ![]() . Первый нетривиальный вариант задачи
наилучшего приближения возникает при N=n+1. Эта задача
известна как задача чебышевского интерполирования.
. Первый нетривиальный вариант задачи
наилучшего приближения возникает при N=n+1. Эта задача
известна как задача чебышевского интерполирования.
Теорема. Для того, чтобы полином ![]() был полиномом наилучшего
приближения для таблицы
был полиномом наилучшего
приближения для таблицы ![]() , необходимо и достаточно, чтобы
при некотором
, необходимо и достаточно, чтобы
при некотором ![]() выполнялось
условие:
выполнялось
условие:
![]() ,
(4.26)
,
(4.26)
что также
гарантирует выполнение равенства ![]() .
.
Доказательство.
Вопрос
о существовании такого полинома ![]() сводится к вопросу о существовании
решения системы линейных уравнений вида, являющейся развернутой записью условия
(4.26).
сводится к вопросу о существовании
решения системы линейных уравнений вида, являющейся развернутой записью условия
(4.26).
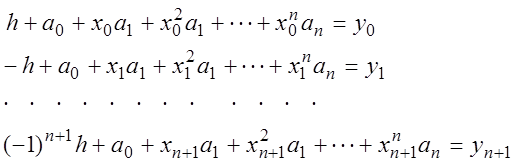 (4.27)
(4.27)![]()
Определитель матрицы этой системы может быть записан в виде:
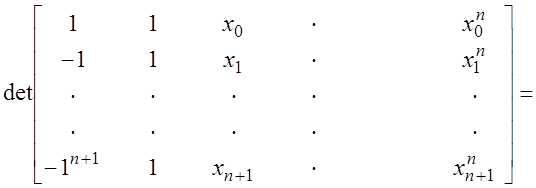
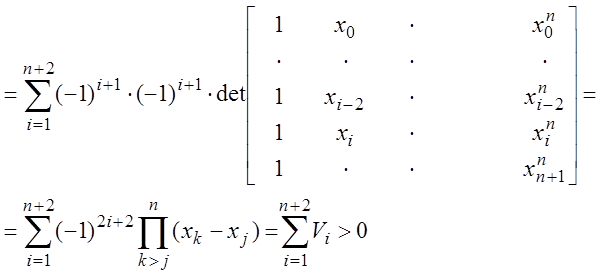
Здесь
![]() - определитель
матрицы Вандермонда, который при
- определитель
матрицы Вандермонда, который при ![]() , очевидно, будет величиной
положительной. Таким образом, приведенная выше система линейных уравнений имеет
единственное решение.
, очевидно, будет величиной
положительной. Таким образом, приведенная выше система линейных уравнений имеет
единственное решение.
Теперь
покажем, что найденный при решении системы (4.27) модуль величины уклонения в
узлах таблицы (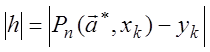 ) равен
) равен![]() . Допустим, что это не так, т.е.
. Допустим, что это не так, т.е.
![]() . Это допущение
означает, что существует полином
. Это допущение
означает, что существует полином ![]() , для которого выполняется неравенство
, для которого выполняется неравенство
![]() (4.28)
(4.28)
Построим
полином ![]() . Для него будет
справедливо следующее выражение:
. Для него будет
справедливо следующее выражение:
![]()
C учетом
неравенства (4.28) можно утверждать, что функция ![]() на конечном интервале
на конечном интервале ![]()
![]() раза изменяет свой знак.
Последнее доказывает существовании у функции n+1 нуля. Но
полином n-го порядка, имеющий на конечном интервале
более nнулей, должен быть тождественно
равным нулю. Таким образом:
раза изменяет свой знак.
Последнее доказывает существовании у функции n+1 нуля. Но
полином n-го порядка, имеющий на конечном интервале
более nнулей, должен быть тождественно
равным нулю. Таким образом:
![]() .
.
Следовательно,
предположение ![]() не верно и
теорема полностью доказана.
не верно и
теорема полностью доказана.
Задача чебышевского интерполирования имеет важное значение для нахождения полинома наилучшего равномерного приближения функции, заданной таблицей при «длине» таблицы N > (n+1). Рассмотрим схему решения этой задачи.
Систему
точек ![]() , где K – множество (n+2) индексов, будем
называть базисом. Другими словами, базис – это упорядоченный по возрастанию
набор из (n+2) точек, каждая из которых
принадлежит множеству задания приближаемой функции. Ясно, что на множестве
, где K – множество (n+2) индексов, будем
называть базисом. Другими словами, базис – это упорядоченный по возрастанию
набор из (n+2) точек, каждая из которых
принадлежит множеству задания приближаемой функции. Ясно, что на множестве ![]() можно построить несколько
базисов. На каждом из них может быть решена задача чебышевского
интерполирования. По отношению к каждому из этих решений (полиному
можно построить несколько
базисов. На каждом из них может быть решена задача чебышевского
интерполирования. По отношению к каждому из этих решений (полиному ![]() ) можно вычислить значение
максимума уклонения на полной таблице
) можно вычислить значение
максимума уклонения на полной таблице
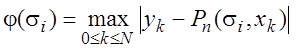
и для него будет справедливо неравенство
![]() .
.
Если для
некоторого базиса ![]() окажется, что
окажется, что
![]() ,
,
то этот полином
чебышевского интерполирования ![]() и является полиномом наилучшего
равномерного приближения функции
и является полиномом наилучшего
равномерного приближения функции ![]() на таблице
на таблице ![]() .
.
Таким образом видно, что проблема построения полинома наилучшего равномерного приближения сводится к построению алгоритма целенаправленного перебора базисов. Критерием такого перебора служит [5] неравенство
![]() .
.
Разработаны
несколько алгоритмов формирования базисов ![]() (в частности, R-алгоритм [5]).
Однако их рассмотрение выходит за рамки курса.
(в частности, R-алгоритм [5]).
Однако их рассмотрение выходит за рамки курса.
Равномерное приближение непрерывной на [a, b] функции имеет много
общих черт с рассмотренной выше задачей. Определение полинома наилучшего
равномерного приближения функции f(x), как полинома ![]() , для которого выполняется
равенство
, для которого выполняется
равенство ![]() , сохраняется,
но нахождение величины
, сохраняется,
но нахождение величины
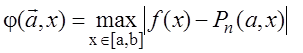 (4.29)
(4.29)
в этом случае
требует решения экстремальной задачи на непрерывном интервале [a, b], а не на дискретном
множестве![]() .
.
Существование и единственность полинома наилучшего равномерного приближения непрерывной на [a, b] функции доказано теоремой Чебышева. Одновременно, этой теоремой доказано, что:
для
того, чтобы полином ![]() был полиномом
наилучшего равномерного приближения на [a, b] непрерывной
функции f(x) необходимо и
достаточно, чтобы он осуществлял чебышевскую интерполяцию на экстремальном
базисе
был полиномом
наилучшего равномерного приближения на [a, b] непрерывной
функции f(x) необходимо и
достаточно, чтобы он осуществлял чебышевскую интерполяцию на экстремальном
базисе ![]() ; при этом
выполняется условие
; при этом
выполняется условие
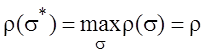
Другими
словами, на интервале [a, b] должна
существовать такая последовательность из (n+2) точек ![]() , в которых справедливы
следующие соотношения
, в которых справедливы
следующие соотношения
![]() (4.30)
(4.30)
Очевидно, что в
точках экстремального базиса функция уклонения ![]() достигает своего модуль-максимума и
последовательно меняет знак (рис. 4.3). Такой
экстремальный базис часто называют чебышевским альтернансом.
достигает своего модуль-максимума и
последовательно меняет знак (рис. 4.3). Такой
экстремальный базис часто называют чебышевским альтернансом.
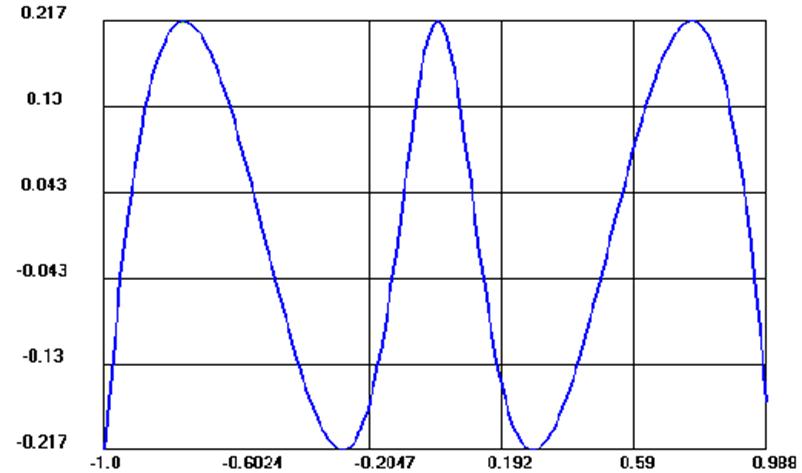
Рис. 4.3. Функция уклонения для задачи наилучшего равномерного приближения функции Рунге полиномом 5-й степени
Аналитически задача наилучшего равномерного приближения непрерывной функции решается в очень ограниченном числе случаев. Один из численных методов ее решения – сеточный, базируется на многократной дискретизации непрерывной функции f(x) на системе все более сгущающихся сеток:
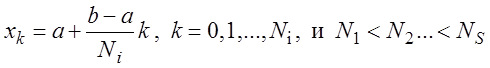
Решения задач наилучшего приближения для дискретизированной функции образуют последовательность полиномов
![]() ,
,
для которых справедливо:
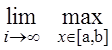
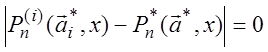 .
.
Одним из наиболее мощных алгоритмов численного построения полинома наилучшего приближения для непрерывной функции является второй полиномиальный алгоритм Ремеза. Ниже приведены его основные этапы.
Ш.1. Положить k = 1 и задать начальный базис ![]()
Ш.2.
Провести чебышевскую интерполяцию, т.е. построить ![]() и определить соответствующее значение
и определить соответствующее значение ![]() .
.
Ш.3. Исследовать функцию ![]() и найти
и найти
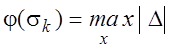
Ш4.
Если![]() , то задача решена,
, то задача решена,
иначе:
Ш5.
Построить новый базис ![]() так, чтобы
так, чтобы
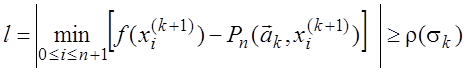
и
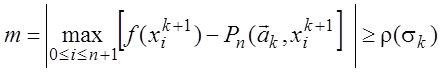 ,
,
при ![]() .
.
Ш.6. k = k+1 и перейти к Ш.2
Отметим две важные детали
реализации этого алгоритма. Первая относится к формированию начального базиса ![]() . Хорошим выбором может служить чебышевская сетка (n+1) порядка на интервале приближения.
. Хорошим выбором может служить чебышевская сетка (n+1) порядка на интервале приближения.
Второй и более серьезной
проблемой является выполнение пятого шага алгоритма. Одним из возможных его
вариантов может быть определение всех экстремальных точек функции ![]() и выбор из их числа координат базиса
и выбор из их числа координат базиса ![]() . В общем случае, решение такой экстремальной задачи является
достаточно трудоемким.
. В общем случае, решение такой экстремальной задачи является
достаточно трудоемким.
В целом, рассмотренный алгоритм обладает высокой скоростью сходимости, что делает его хорошим выбором в практике решения задач равномерного приближения.
4.3.2. Среднеквадратичное приближение функций
Построение приближающего полинома может быть реализовано и на основе среднеквадратичного критерия близости:
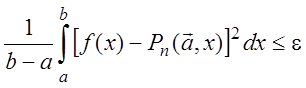 ,
(4.31)
,
(4.31)
где ![]() - приемлемая мера близости.
- приемлемая мера близости.
В
случае функции, заданной на дискретном множестве точек ![]() этот критерий приобретает вид
этот критерий приобретает вид
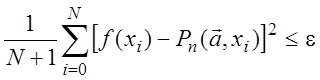 (4.32)
(4.32)
Задача
(4.31) может быть развита в задачу наилучшего среднеквадратичного приближения,
т.е. в задачу построения полинома ![]() , вектор коэффициентов которого
являются решением задачи минимизации функции
, вектор коэффициентов которого
являются решением задачи минимизации функции 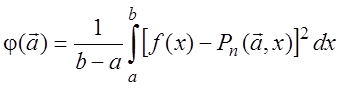 .
.
В
случае функции, заданной на дискретном множестве точек ![]() задача нахождения минимума
функции
задача нахождения минимума
функции
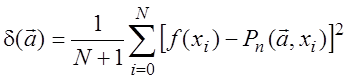
эквивалентна задаче нахождения нормального псевдорешения системы линейных уравнений вида:
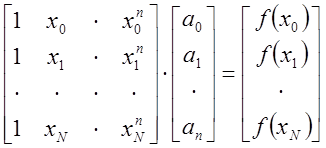 (4.33)
(4.33)
Решение
таких систем посредством сведения их к системам нормальных уравнений, мало
перспективно уже при сравнительно небольших значениях n, что является
следствием близости системы степенных функций к линейно зависимой. В определенном
смысле «наиболее линейно независимой» является система функций ![]() ортогональных на множестве точек
ортогональных на множестве точек ![]() . На интервале [-1,1] примером таких
функций могут служить многочлены Чебышева
. На интервале [-1,1] примером таких
функций могут служить многочлены Чебышева ![]() .
Заметим, что найденный методом наименьших квадратов полином
.
Заметим, что найденный методом наименьших квадратов полином 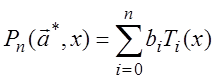 , является лишь иным представлением
полинома наилучшего среднеквадратичного приближения. Вместе с тем, задача вычисления
коэффициентов
, является лишь иным представлением
полинома наилучшего среднеквадратичного приближения. Вместе с тем, задача вычисления
коэффициентов ![]() существенно лучше
обусловлена в сравнении с задачей нахождения коэффициентов
существенно лучше
обусловлена в сравнении с задачей нахождения коэффициентов ![]() обычного алгебраического полинома.
обычного алгебраического полинома.
В заключение заметим, что одним из самых эффективных методом решения задачи наилучшего среднеквадратичного приближения является метод сингулярного разложения (SVR), подробно описанный в [4].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.