



Министерство высшего образования УР.
Удмуртский Государственный Университет.
Кафедра «теплоэнергетики»
Отчёт
по лабораторной работе №1
Выполнил студент гр.34-31
Проверил преподаватель
Ижевск 2005.
Записка:
1. постановка задачи
2. исходные данные
3. решение
4. вывод
1.
В лабораторной работе для
данных уравнений найти ближайший к нулю корень уравнения, с точностью ε, тремя
различными методами, а именно: методом половинного деления, простых итераций и
методом Ньютона. Для метода Дихотомии найти число произведенных итераций
заранее. Сравнить их вычислительную эффективность для данных уравнений ![]() .
.
2. Решить задачу (1) для данных уравнений:
2.1.
![]() ,
где p = 0,2; q
= 0,3
,
где p = 0,2; q
= 0,3
2.2.
![]() ,
где а=
0; b = 1; c = -3.
,
где а=
0; b = 1; c = -3.
2.3. точность ε= 0,0001
3. методы, применяемые для решения задачи (1)
3.1. Дихотомия (деление пополам)
Это метод применяется, если мы имеем только
единственный корень на отрезке [a,b]. Пусть мы нашли такие точки a, b, что
![]() ,
т.е. на отрезке [a,b] лежит не менее одного корня уравнения,
найдем середину отрезка
,
т.е. на отрезке [a,b] лежит не менее одного корня уравнения,
найдем середину отрезка ![]() и
вычислим f(ξ).
Из двух половин отрезка выберем ту, для которой
и
вычислим f(ξ).
Из двух половин отрезка выберем ту, для которой ![]() ,
ибо один из корней лежит на этой половине. Затем новый отрезок опять делим
пополам и выберем ту половину, на концах которой функция имеет разные знаки, и
т.д. Если требуется найти корень с точностью ε, то продолжаем деление
пополам до тех пор, пока длина отрезка не станет меньше заданного значения ε,
в данной задаче равным 0,0001. Дихотомия проста и очень надежна: к простому
корню она сходится для любых непрерывных функций f(x), в том числе недифференцируемых: при этом она
устойчива к ошибкам округления. Скорость сходимости невелика: за одну итерацию
точность увеличивается примерно вдвое. Зато точность ответа гарантируется.
Метод неприменим к корням четной кратности. Для корней нечетной высокой
кратности он сходится, но менее точен и хуже устойчив к ошибкам округления,
возникающих при вычислении f(x). Дихотомия применяется тогда, когда требуется высокая надежность
счета, а скорость сходимости малосущественна.
,
ибо один из корней лежит на этой половине. Затем новый отрезок опять делим
пополам и выберем ту половину, на концах которой функция имеет разные знаки, и
т.д. Если требуется найти корень с точностью ε, то продолжаем деление
пополам до тех пор, пока длина отрезка не станет меньше заданного значения ε,
в данной задаче равным 0,0001. Дихотомия проста и очень надежна: к простому
корню она сходится для любых непрерывных функций f(x), в том числе недифференцируемых: при этом она
устойчива к ошибкам округления. Скорость сходимости невелика: за одну итерацию
точность увеличивается примерно вдвое. Зато точность ответа гарантируется.
Метод неприменим к корням четной кратности. Для корней нечетной высокой
кратности он сходится, но менее точен и хуже устойчив к ошибкам округления,
возникающих при вычислении f(x). Дихотомия применяется тогда, когда требуется высокая надежность
счета, а скорость сходимости малосущественна.
Решим первое уравнение, применив дихотомию для нахождения корня:
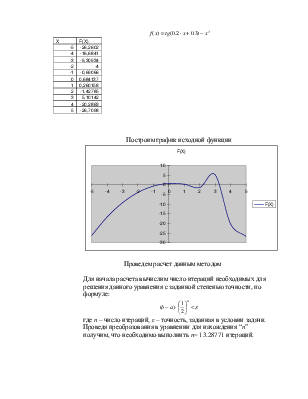
![]()
|
X |
F(X) |
|
-5 |
-26,2602 |
|
-4 |
-16,6841 |
|
-3 |
-9,30934 |
|
-2 |
-4 |
|
-1 |
-0,69066 |
|
0 |
0,684137 |
|
1 |
0,260158 |
|
2 |
-1,42785 |
|
3 |
5,10142 |
|
4 |
-20,2863 |
|
5 |
-26,7098 |
Построим график исходной функции
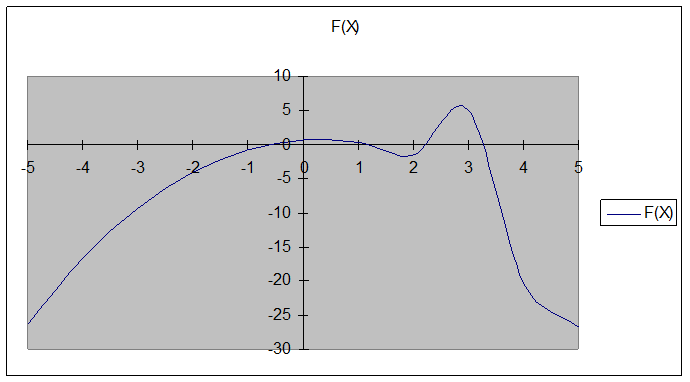
Проведем расчет данным методом
Для начала расчета вычислим число итераций необходимых для решения данного уравнения с заданной степенью точности, по формуле:
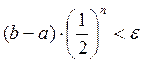
где n – число итераций, ε – точность, заданная в условии задачи.
Проведя преобразования в уравнении для нахождения “n” получим, что необходимо выполнить n= 13.28771 итераций.
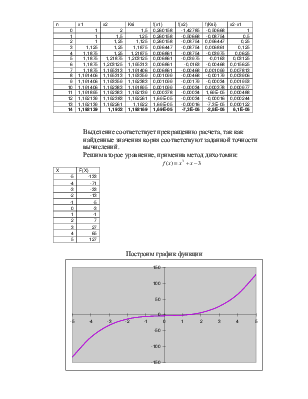
|
n |
x1 |
x2 |
Ksi |
f(x1) |
f(x2) |
f(Ksi) |
x2-x1 |
|
0 |
1 |
2 |
1,5 |
0,260158 |
-1,42785 |
-0,50668 |
1 |
|
1 |
1 |
1,5 |
1,25 |
0,260158 |
-0,50668 |
-0,08754 |
0,5 |
|
2 |
1 |
1,25 |
1,125 |
0,260158 |
-0,08754 |
0,096447 |
0,25 |
|
3 |
1,125 |
1,25 |
1,1875 |
0,096447 |
-0,08754 |
0,006861 |
0,125 |
|
4 |
1,1875 |
1,25 |
1,21875 |
0,006861 |
-0,08754 |
-0,03975 |
0,0625 |
|
5 |
1,1875 |
1,21875 |
1,203125 |
0,006861 |
-0,03975 |
-0,0163 |
0,03125 |
|
6 |
1,1875 |
1,203125 |
1,195313 |
0,006861 |
-0,0163 |
-0,00468 |
0,015625 |
|
7 |
1,1875 |
1,195313 |
1,191406 |
0,006861 |
-0,00468 |
0,001099 |
0,007813 |
|
8 |
1,191406 |
1,195313 |
1,193359 |
0,001099 |
-0,00468 |
-0,00179 |
0,003906 |
|
9 |
1,191406 |
1,193359 |
1,192383 |
0,001099 |
-0,00179 |
-0,00034 |
0,001953 |
|
10 |
1,191406 |
1,192383 |
1,191895 |
0,001099 |
-0,00034 |
0,000378 |
0,000977 |
|
11 |
1,191895 |
1,192383 |
1,192139 |
0,000378 |
-0,00034 |
1,69E-05 |
0,000488 |
|
12 |
1,192139 |
1,192383 |
1,192261 |
1,69E-05 |
-0,00034 |
-0,00016 |
0,000244 |
|
13 |
1,192139 |
1,192261 |
1,1922 |
1,69E-05 |
-0,00016 |
-7,3E-05 |
0,000122 |
|
14 |
1,192139 |
1,1922 |
1,192169 |
1,69E-05 |
-7,3E-05 |
-2,8E-05 |
6,1E-05 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.