Исследование на сходимость СЛАУ. Система линейных уравнений. Метод Гаусса для решения СЛАУ

Министерство высшего образования УР.

Удмуртский Государственный Университет.

Кафедра «теплоэнергетики»

Отчёт

 по лабораторной работе №2

Выполнил студент гр.34-31

Проверил преподаватель

Ижевск 2005.

Постановка задачи

Исследовать на сходимость данную систему линейных алгебраических уравнений (СЛАУ) Ax = b и решить итерационным методом в форме Якоби. Результат сравнить с методом Гаусса.

      Исходные данные

Система линейных уравнений

Метод Гаусса для решения СЛАУ

1.1 Метод

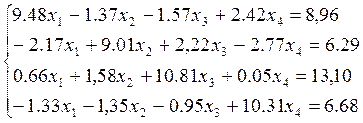
Наиболее распространенным методом решения СЛАУ является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных. Существуют различные схемы, реализующие этот метод. Рассмотрим одну из них – схему единственного деления.

Для простоты ограничимся рассмотрением системы четырех уравнений с четырьмя неизвестными

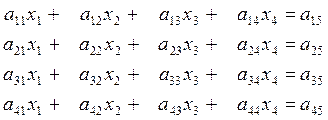
Пусть  (ведущий элемент). Разделив первое уравнение системы на  получим

   (*)

Где 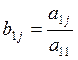 (j=2,3,4,5).

Пользуясь уравнением (*), можно исключить неизвестное x₁ из второго, третьего и четвертого уравнений системы. Для этого следует умножить уравнение (*) на a₂₁, a₃₁ и a₄₁ и вычесть результаты соответственно из второго, третьего и четвертого уравнений системы.

В результате получим систему трех уравнений:

 (**)

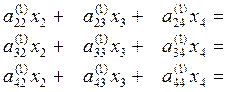
Где коэффициенты  вычисляются по формуле

 (i=2,3,4; j=2,3,4,5).

Далее первое уравнение системы (**) делим на , получим

     (***)

Где 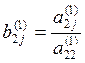 (j=3,4,5)

Исключая теперь x₂ так же, как мы исключали x₁, получим систему уравнений

Разделив первое уравнение системы на  получим

Где 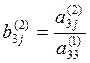 (j=4,5)

С помощью этого уравнения исключим x₃ из второго уравнения системы. Получим уравнение

Таким образом, первоначальную систему мы привели к эквивалентной системе с треугольной матрицей:

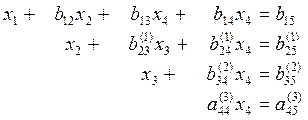
Откуда последовательно находим

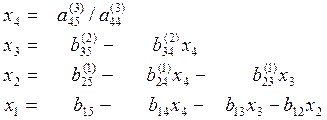
Итак, решение системы распадается на два этапа:

Прямой ход

·  Приведение начальной системы к треугольному виду

Обратный ход

·  Определение неизвестных по формулам

Рассмотренный метод применим лишь при условии, что все ведущее элементы отличны от нуля.

Решим данную нам СЛАУ методом Гаусса

 

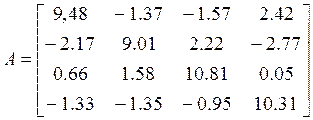
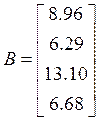
Решение.

Прямой ход. Разделив первое уравнение системы на а₁₁= 9,48 получим:

Вычисляем  коэффициенты  и составляем систему при i=2:

 8.698         

1.86

 -2.217        

8.34

Вычисления при i=3

1.675

10.919

-0.118

12.476

Вычисления при i=4

-1.541

-1.17

10.649

7.937

Таким образом, получаем систему с тремя неизвестными:

8.698x2	+1.86x3	-2.217x4	= 8.34
1,675x2	+10.919x3	-0.118x4	= 12,476
-1.541x2	-1.17x3	10.649x4	= 7.937

Разделив первое уравнение полученной системы на  записываем:

Вычисляем  коэффициенты  и составляем систему при i=3

 11,277           

0,309

10,869

Вычисления при i=4.

-1,499

10,256

9,414

Записываем систему с двумя неизвестными:

11,277x3	+0,309x4	= 10,869
-1,499x3	+10,256x4	= 9,414

Разделив первое уравнение этой системы на , получаем

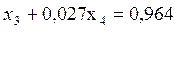
Находим коэффициенты :

10,296

10,859

И записываем одно уравнение с одним неизвестным:

Таким образом, эквивалентная система имеет вид

На этом прямой ход заканчивается.

Обратный ход

последовательно из полученных систем находим

,05          

           

2.  метод Якоби

2..1  теория метода

для того чтобы применить метод простой итерации к решению СЛАУ  с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду

Здесь В – квадратная матрица с элементами b_ij (i,j=1,2,…m); c – вектор – столбец с элементами с_i(i=1,2,…m).

В развернутой форме записи система имеет следующий вид:

…………………………………….

Как правило, операция приведения системы к виду, удобному для итерации не является простой и требует специальных знаний, а также существенного использования специфики системы.

2.2.описание метода простой итерации

выберем начальное приближение . Подставляя его в правую часть системы и вычисляя полученное выражении, находим первое приближение

Подставляя приближение x⁽¹⁾ в правую часть системы, получаем

Продолжая этот процесс далее, получаем последовательность  приближений, вычисляемых по формуле

 k=0,1,2,…(*)

2.3.сходимость метода простой итерации

если , то условие  принимает вид

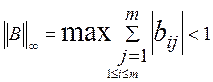
Для метода Якоби это условие в силу равенств b_ii=0, b_ij=-a_ij/a_ii для  эквивалентно условию строчного диагонального преобладания. Таким образом для сходимости метода Якоби достаточно, чтобы матрица А была близка к диагональной.

2.4.Апостериорная оценка погрешности метода Якоби

Если выполнено условие , то справедлива апостериорная оценка погрешности

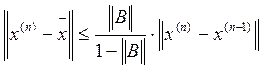
- это норма вектора, согласованного с нормой матрицы

=

= 1,27353

= 0,34835

= 0,09529

= 0,02606

= 0,00713

= 0,00195

Далее расчет прекращается, т.к. оценка меньше ε₁

В качестве критерия окончания итерационного процесса может быть использовано неравенство

 (**)

Где 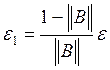, а ε = 0,01/2 = 0,005

2.1  Решение системы методом простой итерации в форме Якоби

Вычислив коэффициенты по формулам (*) приведем систему к виду:

x1=	0,000x1	+0,145x2	+0,166x3	-0,255x4	=	0,945
x2=	0,241 x1	+0,000x2	-0,246 x3	+0,307x4	=	0,698
x3=	-0,061 x1	-0,146 x2	+0,000x3	-0,005 x4	=	1,212
x4=	0,129 x1	+0,131x2	+0,092x3	+0,000x4	=	0,648

В последнем уравнении коэффициенты даны с точностью до погрешности округления. Здесь

    

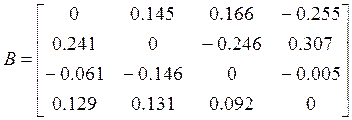
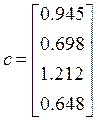
Достаточное условие сходимости метода простой итерации выполнено, так как

Примем за начальное приближение к решению вектор  и будем вести итерации по формуле (*) до выполнения критерия окончания (**), где в данном случае =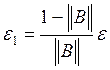

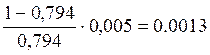
Результаты расчета приведены в таблице, значения приближения приводятся с пятью цифрами после десятичной точки.

n	X1	X2	X3	X4	||B||/(1-||B||)*||Xn-Xn-1||	||Xn-Xn-1||∞
1	1,500	1,500	1,500	1,500	-	-
2	1,029	1,301	0,894	1,046	0,256	0,471
3	1,015	1,137	0,954	0,951	0,007	0,014
4	1,026	1,095	0,979	0,928	0,014	0,025
5	1,030	1,087	0,985	0,924	0,003	0,006
6	1,031	1,086	0,986	0,923	0,001	0,001

При n = 6 условие (**) выполняется и можно положить

        

        

3.  Вывод

Основным недостатком метода Гаусса является то, что при большом числе неизвестных линейной системы схема, дающая точное решение становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться методом простых итераций. Если метод итераций сходится, он дает следующие преимущества по сравнению с методом Гаусса:

·  Если итерации сходятся достаточно быстро, то есть если для решения