Ближайший к нулю корень уравнения, с точностью ε, тремя различными методами. Методы, применяемые для решения задачи, страница 2

Выделение соответствует прекращению расчета, так как найденные значения корня соответствуют заданной точности вычислений.

Решим второе уравнение, применив метод дихотомии:

Построим график функции

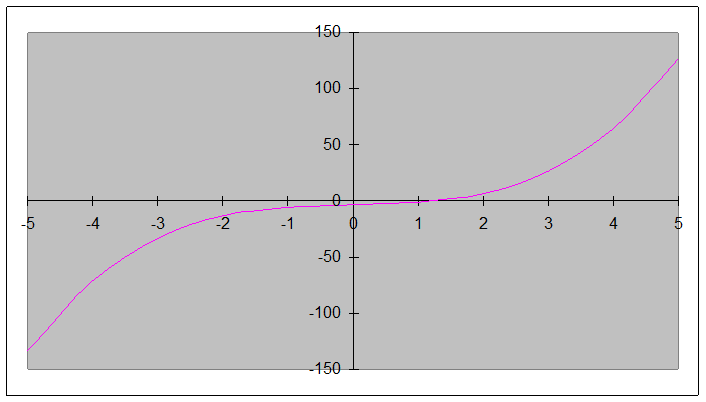
Проведем расчет данным методом

Для начала расчета вычислим число итераций необходимых для решения данного уравнения с заданной степенью точности, по формуле:

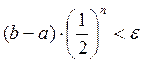
где n – число итераций, ε – точность, заданная в условии задачи.

Проведя преобразования в уравнении для нахождения “n” получим, что необходимо выполнить n=13.28771 итераций.

Выделение соответствует прекращению расчета, так как найденные значения корня соответствуют заданной точности вычислений.

3.2.  Метод простых итераций

Заменим уравнение вида y = f(x) эквивалентным ему уравнением x=φ(x). Это можно сделать многими способами, например, положив , где ψ(x) – произвольная непрерывная знакопостоянная функция. Выберем некоторое нулевое приближение x₀  и вычислим дальнейшие приближения по формулам:

 n=0, 1, 2, …

Очевидно, если x_n стремится к некоторому пределу , то этот предел есть корень исходного уравнения. Оценка метода определяется по формуле:

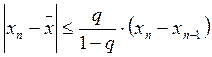
Где  

Решим первое уравнение, применив метод простых итерации  для нахождения корня:

Найдем q

Т. к. q – максимальное значение производной и меньше 1, то из таблицы следует, что q=0,7764