Математика \ Математика

Ближайший к нулю корень уравнения, с точностью ε, тремя различными методами. Методы, применяемые для решения задачи, страница 3

n

x

Fi(x)

q

q/(1-q)

IXn-Xn-1I

произведение

эпсилон

сравнение

0

2

1,603793

0,7764

3,472272

0,0001

1

1,603793

1,369799

3,472272

0,396207114

1,375738833

0,0001

нет

2

1,369799

1,263144

3,472272

0,233993514

0,812489106

0,0001

нет

3

1,263144

1,219655

3,472272

0,10665514

0,370335648

0,0001

нет

4

1,219655

1,202679

3,472272

0,043489434

0,151007141

0,0001

нет

5

1,202679

1,196162

3,472272

0,016975976

0,058945203

0,0001

нет

6

1,196162

1,193676

3,472272

0,006516814

0,022628151

0,0001

нет

7

1,193676

1,19273

3,472272

0,002485858

0,008631574

0,0001

нет

8

1,19273

1,192371

3,472272

0,00094595

0,003284595

0,0001

нет

9

1,192371

1,192234

3,472272

0,000359634

0,001248749

0,0001

нет

10

1,192234

1,192182

3,472272

0,000136679

0,000474588

0,0001

нет

11

1,192182

1,192162

3,472272

5,19382E-05

0,000180344

0,0001

нет

12

1,192162

1,192155

3,472272

1,97356E-05

6,85272E-05

0,0001

да

Выделение соответствует прекращению расчета, так как найденные значения корня соответствуют заданной точности вычислений.

Решим второе уравнение, применив метод простых итераций:

Найдем q.

Для этого построим график f’(x)

X

F(X)

1

3

1,2

3,6

1,3

3,9

1,4

4,2

1,5

4,5

1,6

4,8

1,7

5,1

1,8

5,4

1,9

5,7

2

6

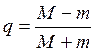, где М = 6 – max f'(x), m = 3 – min f'(x), тогда q = 0.3333

n

x

Fi(x)

q

q/(1-q)

IXn-Xn-1I

эпсилон

сравнение

0

1

1,259918

0,3333

0,499925

0,0001

1

1,259918

1,202788

0,499925

0,259918

0,129939577

0,0001

нет

2

1,202788

1,21581

0,499925

0,05713

0,028560778

0,0001

нет

3

1,21581

1,212866

0,499925

0,013022

0,006509843

0,0001

нет

4

1,212866

1,213533

0,499925

0,002943

0,001471509

0,0001

нет

5

1,213533

1,213382

0,499925

0,000667

0,00033325

0,0001

нет

6

1,213382

1,213416

0,499925

0,000151

7,54385E-05

0,0001

да

Выделение соответствует прекращению расчета, так как найденные значения корня соответствуют заданной точности вычислений.

3.3.  Метод Ньютона (метод касательных)

Пусть дано нелинейное уравнение f(x)=0 и пусть а интервале изоляции [x1,a] производные f’(x) и f”(x) непрерывны и сохраняют определенные знаки. В качестве начального приближения выбираем конец интервала изоляции, на котором знаки f(x) и f”(x) совпадают. Формула метода Ньютона имеет вид:

Скачать файл