Градиент скалярного поля. Частные дифференциалы. Геометрический смысл. Двойной интеграл. Основные понятия и определения

1вопрос:Областью определения ф,на-ют множество знач(x1,x2,xn),при ко-ых определенна.Множество значений ф.-множетво значений, ко-ая принимает ф.y. Графиком  ф z=f(x,y)яв-ся поверхность.,на-ся множество (.)ек пространства абцисса и ордината, ко-ых принимает значения x,y из области определ, а аппликата значения ф. z

Линиями уровня ф 2ых переменных,на-ют множество (.)ек на плоскости, в ко-ых ф.принимает const значения. Если это значение равно I, то линии уровня С. По линиям уровня судят об изменении ф. Окрестностью (.)М0(x0,y0),на-ся множество (.)ек плоскости(x,y),лежащих внутри круга R=δ. 2вопрос: Частной производной ф z по x,на-ся lim отношения частного приращения z по x к этому приращению, если Δx0,т.е.

;

3вопрос:

Частными дифференциалами ф 2ых переменных, на-ют произведения частной производной на соответствующей дифференциал переменной

Полной диффер ф 2ых переменных, на-ют сумму частных дифф

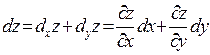Геометрический смысл: частная производная ф по x в (.) (x0,y0) равна tg α угла наклона касательной, преденной к кривой плоскости y=const в (.) (x0,y0). 4вопрос:

Как и в случае одной переменной  полной дифференциал, есть линейная часть полного приращения ф. Пренебрегая б.м.в. можно получить формулу:

5вопрос:

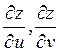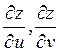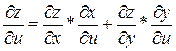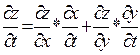6вопрос:Если ф z=f(x,y) – сложная ф., где x=x(u,v), y=y(u,v); u,v- независимые переменные, то чтобы найти  существует 2 способа:1.Подставить x;y в ф.z, найти x=x(u,v),y=y(u,v) в z=f(x,y);2.из формулы полого приращения, далее на Δu: и аналогично выводитсяЕсли ф z=f(x,y) ,где x=x(t),y=y(t),то z-одной переменной. Если z=f(x,y), где y=y(x), то формула полной производной

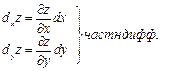7вопрос: Производная неявной заданной ф.1.)Пусть F(x,y)=0 y=y(x), 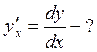Пусть z=F(x,y)=0, y=y(x),тогда применим последнюю выведенную формулу: , с другой стороны т.к. z=0,то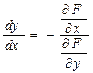2.F(x,y,z),z=z(x,y), 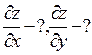применим полученную формулу:

А) при y=const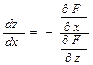

Б) при x=const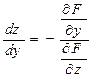

8вопрос: Производная по направлению. Скалярным полем, на-ют ф. нескольких переменных, определенную в некоторой области. при n=2:ф.z=z(x,y)-плоское скалярное поле ;при n=3 ф.u=u(x,y,z)-пространственное скалярное поле; рассмотрим плоское скалярное поле z=z(x,y),выберем,М₀(x₀,y₀), в ко-ой ф. дифференцируема, тогда производной по направлениюданной ск поля М_0,на-ют(предел отношения приращению модуля направления, если последние стремится к нулю)

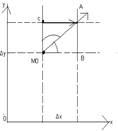Выведем ф. для выч произв по направлению плоск ск поля

Пусть направления l задается с помощью, направляющих сos:

В ΔM₀AB

В ΔM₀CA:т.к. ф. z=z(x,y) дифференцируема в M₀, то её приращение можно представить в виде: , где α₁,α₂-б.м.в. при ,;разделим рав-во наΔl:

Формула для вычисления производной по направлению:аналогично и справедливо для n-мерного поля, в случае пространственного ск. Поля u=u(x,y,z)

Cosα, cosβ, cosγ- напр. Cos; Если , тоПроизводная по направлению характеризует скорость изменения ск. Поля в (.) ке: если f’(x)>0, то поле в этой (.)ке со скоростью равной модулю f’(x) по направлению

f’(x)>0, то поле

9 вопрос: Градиент скалярного Поля. Рассмотрим простр ск поле u,u=u(x,y,z) тогда вектор

либо:Если градиент определен в каждой (.)ке ск. Поля, то говорят, что ск. Поле порождает векторное поле – поле градиентов. Теорема№1.Произвоидная по направлению равна проекции градиента ск. Поля на это направление, т.е.;док-во: найдем ск. Произведение =* (Cosα, cosβ, cosγ)=

С другой стороны, =

 или  ч.т.д. следствие№1.Производная по направлению достигает своего наибольшего значения по направлению поля, наименьшего значения по направ.- поля. Следствие2. Производная по направлению к касательной к линиям уровня равна нулю. Теорема№2 Градиент пл. ск поля к линиям уровня в этой (.)ке. Следствие из теоремы: u=u(x,y,z)=с, можно записать в виде

10 вопрос:1)Пусть поверх S

Задана Ур-ем z=F(x,y)=0, тогда=Ур-ие пл,проходящей через (.)ку М₀(x₀,y₀) имеет вид:

Сл-но Ур-ие касс к поверх z=F(x,y)=0 в М₀(x₀,y₀)т.к. каноническое Ур-ие прямой , проходящей через (.) M0, параллельно имеет вид:, то Ур-ие нормали к поверхности z=F(x,y)=0 в М_0: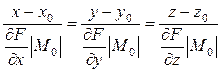

2) Поверхн S зад ур-ем z=f(x,y) S:f(x,y)=z=0

F(x,y,z);; ; Ур-ие касательной пл. в M0

 формула к поверхности f(x,y)=z в М₀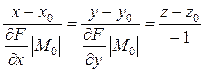

11 вопрос:Если в окрестности некоторой (.)М₀(x₀,y₀) выполняется ра-во f(x0,y0)>f(x,y), где € D: М₀-(.)кА max;или f(x0,y0)<(x,y), где(x,y) € Окр. М_0, то М₀-(.)кА min;(.) max и (.) min – на-ся (.)ми экстремума . Теорема№1.(нач.усл. экстр ф 2ых переменных)Если (.)М₀(x₀,y₀) яв-ся(.)экстремума дифференцируемой в окрестности М₀ функции f(x,y)=z, то или не существует; до-во: