28 вопрос: Диффер Ур., допускающие понижения порядка вида ![]() решается последовательным
интегрированием. Умножая обе части на dx и интегрируя, получаем уравнение (n-1)-го
порядка:
решается последовательным
интегрированием. Умножая обе части на dx и интегрируя, получаем уравнение (n-1)-го
порядка:![]() . Снова умножая обе части на dx и
интегрируя, получаем уравнение (n-2)-го порядка:
. Снова умножая обе части на dx и
интегрируя, получаем уравнение (n-2)-го порядка:![]() и
т.д. После n-кратного интегрирования получаем общий интеграл y этого
уравнения в виде явной ф. от x и n произвольной постоянных:
и
т.д. После n-кратного интегрирования получаем общий интеграл y этого
уравнения в виде явной ф. от x и n произвольной постоянных:![]() .
.
29 вопрос: Диффер Ур., допускающие понижения порядка вида![]()
![]() (не содержит явно y)
(не содержит явно y)![]() решаем с помощью замены переменной
решаем с помощью замены переменной
![]() подставляем в Ур-ие
подставляем в Ур-ие![]() -
Ур-ие 1ого порядка в завис от вида Ур-ия находим его общие решение.
-
Ур-ие 1ого порядка в завис от вида Ур-ия находим его общие решение.![]() вернемся к
вернемся к ![]() ,
,
![]()
![]() общие
решение исходного Ур-ия.
общие
решение исходного Ур-ия.
30 вопрос: Диффер Ур., допускающие понижения порядка вида
![]()
![]() (не явно заданна x)решаем с
помощью замены переменной
(не явно заданна x)решаем с
помощью замены переменной ![]() =
=
![]()
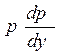 подставляем
в Ур-ие:
подставляем
в Ур-ие: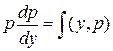 - Ур-ие 1ого порядка в зависимости
от его вида решаем и получаем общий интеграл
- Ур-ие 1ого порядка в зависимости
от его вида решаем и получаем общий интеграл ![]() (или
(или![]() ) т.к.
) т.к. ![]() ,
то получили
,
то получили ![]() - ур-ие 1ого порядка. После его
решения получили общий интеграл ур-ие:
- ур-ие 1ого порядка. После его
решения получили общий интеграл ур-ие: ![]() .
.
31 вопрос: Диффер Линейные Ур-ия высших порядков. Линейным
Дифф n-ого порядка, на-ся Ур-ие, содержащие ![]() и линейное относительно них, т.е.
и линейное относительно них, т.е. ![]() , где b0(x),b1(x),..b(x),f(x):(b0(x)
, где b0(x),b1(x),..b(x),f(x):(b0(x)![]() 0)- коэффициенты непрерывности ф. или константы.;
разделим уравнение на b0(x) и обозначим
0)- коэффициенты непрерывности ф. или константы.;
разделим уравнение на b0(x) и обозначим ![]() тогда
Ур-ие запишется в приведенном виде:
тогда
Ур-ие запишется в приведенном виде:![]() ●Если q(x)=0, то
Ур-ие
●Если q(x)=0, то
Ур-ие ![]() , то Ур-ия на-ся линейным
однородным n порядка; ●Если q(x)
, то Ур-ия на-ся линейным
однородным n порядка; ●Если q(x) ![]() 0, то ур.
0, то ур. ![]() , на-ся
линейным не однородным ур-ем 1ого порядка.
, на-ся
линейным не однородным ур-ем 1ого порядка.
32 вопрос: Линейных однородных дифференциальных ур-ий
2ого порядка. Вид общего решения. р/м Линейных однородных дифференциальных
ур-ий 2ого порядка:![]() (1)
(1)
Теорема№1. Если y=y1(x),y=y2(x)-решение
ур. (1), то ф.![]() - также решение ур-ия (1) Следствие№1.
Если y=y1(x)-реш (1),то
- также решение ур-ия (1) Следствие№1.
Если y=y1(x)-реш (1),то
![]() - реш (1),
- реш (1),![]() Следствие№2.
Если
Следствие№2.
Если 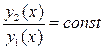 , то y=y1(x),y=y2(x)-линейно.
Не зависим.; Если
, то y=y1(x),y=y2(x)-линейно.
Не зависим.; Если ![]() , то y=y1(x),y=y2(x)-линейно
не зависимы. Средством изучение завис и независ ф. при решении Дифф. Ур-ия
служит определитель Вронского.(Вронскиан):
, то y=y1(x),y=y2(x)-линейно
не зависимы. Средством изучение завис и независ ф. при решении Дифф. Ур-ия
служит определитель Вронского.(Вронскиан):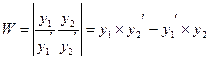 .
.
Теорема№2. Если y=y1(x),y=y2(x)-линейно
завис. Ф., то W=0 Теорема№3. Если при x=x0, ![]() W
W![]() 0, то не равен нулю в любой (.)Ки этого отрезка (т.е.
для любо
0, то не равен нулю в любой (.)Ки этого отрезка (т.е.
для любо ![]() , W
, W![]() 0), где y1,y2 реш. (1).
Следствие№3. Если в любой (.)ке
0), где y1,y2 реш. (1).
Следствие№3. Если в любой (.)ке ![]() W=0, то он
равен 0 в любой (.)ке отрезка, (т.е. W(x)=0 любой
W=0, то он
равен 0 в любой (.)ке отрезка, (т.е. W(x)=0 любой![]() ),
где y=y1,y=y2- реш. (1).
Теорема№4. Если ф. y1(x),y2(x)-линейно не завис на
),
где y=y1,y=y2- реш. (1).
Теорема№4. Если ф. y1(x),y2(x)-линейно не завис на ![]() ,
то W
,
то W![]() 0. Теорема№5(о структуре общего решения
линейного однородного Дифф ур-ия 2ого порядка) Пусть y=y1(x),y=y2(x)-линейно
не зависимые решения ур-ия . (1).,
тогда
0. Теорема№5(о структуре общего решения
линейного однородного Дифф ур-ия 2ого порядка) Пусть y=y1(x),y=y2(x)-линейно
не зависимые решения ур-ия . (1).,
тогда ![]() - общ. решение ур-ия (1). (Замечание: не существует общих
методов решения ур-ия с переменными коэффиц-ми.)
- общ. решение ур-ия (1). (Замечание: не существует общих
методов решения ур-ия с переменными коэффиц-ми.)
33 вопрос: Интегрирование линейных однородных
дифференциальных ур-ий 2ого порядка. р/м линейных однородных дифференциальных
ур-ий 2ого порядка![]()
![]()
Будем искать решение
этого Ур-ия в виде:![]() . Подставим
. Подставим ![]() в ур-ие
в ур-ие
![]()
![]()
![]() т.к.
т.к. ![]() ,
то
,
то ![]() - характеристическое ур-ие. В
зависимости от его корней общее решение исходного ур-ия имеет различный вид:1)
имеет действ. Различные корни, то
- характеристическое ур-ие. В
зависимости от его корней общее решение исходного ур-ия имеет различный вид:1)
имеет действ. Различные корни, то ![]() ;2)имеет
действительные равны корни, то
;2)имеет
действительные равны корни, то ![]()
3)имеет комплексные корни k
![]()
34 вопрос: Интегрирование линейных однородных дифференциальных ур-ий n-ого порядка c постоянными коэфф-ми. р./м линейных однородных дифференциальных ур-ий n-ого порядка c постоянными коэфф-ми.
![]()
![]() -линейн. Не зав. частные реш ур-ия,
по теореме№5 можно записать, что общее решении имеет вид:
-линейн. Не зав. частные реш ур-ия,
по теореме№5 можно записать, что общее решении имеет вид: ![]()
. В зависимости от
корней хар. Ур-ия ![]()
1) Каждому простому
действ. Корню неповторяющему соответствует ![]() ,
,
![]() ; 2)если хар. Ур-ие имеет m
одинаковых дейст-x корней (корень кратности m), то
; 2)если хар. Ур-ие имеет m
одинаковых дейст-x корней (корень кратности m), то ![]() ,
,![]() ,
,
,
,![]() ;
;
3)Каждой паре комплексно-сопряжённых корней
![]() соответствует
соответствует![]() ; 4)если хар. Ур-ие кратные комплексно сопряжённых
числа
; 4)если хар. Ур-ие кратные комплексно сопряжённых
числа ![]() и т.д.), то
и т.д.), то ![]()
![]()
35 вопрос: Линейное неоднородное Диффер ур-ие 2ого
порядка. р/м ![]()
Теорема№1 ( о
структуре лин неодн ур 2ого поряд). Если ![]() -
общее реш од д ур.
-
общее реш од д ур. ![]() ;
;![]() -
частное решение неоднородного Диффер ур-ия
-
частное решение неоднородного Диффер ур-ия ![]() ,
то общие решение неоднородного Диффер ур-ия имеет вид: y=
,
то общие решение неоднородного Диффер ур-ия имеет вид: y=![]() +
+![]() .
Теорема2. Если
.
Теорема2. Если ![]() - о.р.н.д.ур.
- о.р.н.д.ур. ![]() ,
,
![]() - о.р.н.д.ур.
- о.р.н.д.ур. ![]() , то y=
, то y=![]() +
+![]() - о.р.н.д.ур.
- о.р.н.д.ур. ![]() . Замечание. Если правая часть
представляет сумму ф., то необходимо найти общие решение для ур-ий с каждой
ф., а результаты сложить.
. Замечание. Если правая часть
представляет сумму ф., то необходимо найти общие решение для ур-ий с каждой
ф., а результаты сложить.
36 вопрос: Решение не однородного линейного Диффер. 2ого
порядка с правой частью специального вида.1.![]()
![]()
1. ![]() , тогда, где Qn(x)-многочлен
степени n, r=кратности числа α корням характеристического
уравнения
, тогда, где Qn(x)-многочлен
степени n, r=кратности числа α корням характеристического
уравнения
●r=0, если α корням характеристического ур-ия
● r==1, если
α=k1, α![]() k2
k2
● r=2, если
α= k1= k2. Замечание: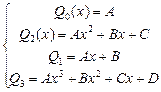
Если правая часть
ур-ия имеет вид![]() , тогда: 1)если число
, тогда: 1)если число ![]() не явл. Корнем характеристического ур-ия (
не явл. Корнем характеристического ур-ия (![]()
![]() k1,2), то
k1,2), то ![]() , где M(x), N(x)-многочлены
степени наивысшей мн-н.
, где M(x), N(x)-многочлены
степени наивысшей мн-н.
2) если ![]() явл корнями хар. Ур (
явл корнями хар. Ур (![]() =k1,2), то
=k1,2), то ![]() .
Частный случай
.
Частный случай ![]()
![]()
(●r=0, если ![]()
![]() k1,2, ●r=0, если
k1,2, ●r=0, если ![]() =k1,2)
=k1,2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.