Р/м ![]() т.к. y=const, то
т.к. y=const, то ![]() - ф-ия 1ой переменной, для которой спр-во
необходимое условие экстремума, т.е.
- ф-ия 1ой переменной, для которой спр-во
необходимое условие экстремума, т.е. ![]() или не
существует. Ч.т.д.;(.)Ки в которых частные производные обращаются в 0 или не
сущ., на-ся критическими, это внутренние (.)Ки области определения .Это
условие не явл-ся достаточным определения экстремума. Теорема№2
(«Достаточное условие функции 2ых переменных» )Пусть (.)М0(x0,y0) такая , что в её окрестности функции. f(x,y)=z
непрерывна вместе с частными производными 1го порядка и
или не
существует. Ч.т.д.;(.)Ки в которых частные производные обращаются в 0 или не
сущ., на-ся критическими, это внутренние (.)Ки области определения .Это
условие не явл-ся достаточным определения экстремума. Теорема№2
(«Достаточное условие функции 2ых переменных» )Пусть (.)М0(x0,y0) такая , что в её окрестности функции. f(x,y)=z
непрерывна вместе с частными производными 1го порядка и ![]() или не сущ;
или не сущ; ![]() , не сущ., тогда если
, не сущ., тогда если
![]()
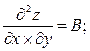
![]() ; и 1)AC-B2>0,A>0,то М0-(.)кА min;2) AC-B2>0,A<0,то М0-(.)кА max; 3) AC-B2<0, то в М0- нет экстремума
(минимакс); 4) AC-B2=0, не известно, есть или нет.
; и 1)AC-B2>0,A>0,то М0-(.)кА min;2) AC-B2>0,A<0,то М0-(.)кА max; 3) AC-B2<0, то в М0- нет экстремума
(минимакс); 4) AC-B2=0, не известно, есть или нет.
12 вопрос: Нахождение наибольшего и наименьшего значения
ф. в замкнутой области: 1. Построить область Д; 2. Найти критические (.)Ки, в
которых 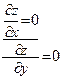 если нет (.)ек, то концах смотрим
значение; 3. Найти знач в кр т, на границах области; 4. Выбрать получ значен
наиб и наим; 5. Ответ:zнаиб(;)=:zнаим(;)=
если нет (.)ек, то концах смотрим
значение; 3. Найти знач в кр т, на границах области; 4. Выбрать получ значен
наиб и наим; 5. Ответ:zнаиб(;)=:zнаим(;)=
 14 вопрос: Метод наименьших квадратов: Это метод
предназначен для сглаживания экспериментальных результатов. Пусть в процессе
получили набор значений (x1,y1),
(x2,y2)…(xn,yn). Запишем в таблицу и отметим. Метод
н.кв.состоит в том, чтобы при определении сглаживающий ф. сделать сумму
квадратов погрешности наименьшая.
14 вопрос: Метод наименьших квадратов: Это метод
предназначен для сглаживания экспериментальных результатов. Пусть в процессе
получили набор значений (x1,y1),
(x2,y2)…(xn,yn). Запишем в таблицу и отметим. Метод
н.кв.состоит в том, чтобы при определении сглаживающий ф. сделать сумму
квадратов погрешности наименьшая.![]() - погрешность;
Определим: как находить параметры сглаживающий ф, если она линейная: Пусть y=a*x+b
- погрешность;
Определим: как находить параметры сглаживающий ф, если она линейная: Пусть y=a*x+b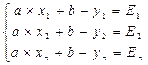 Составим ф.
Составим ф.![]()
![]()
![]()
![]() Найдем локальный min этой
ф.; неизвестные a,b:
Найдем локальный min этой
ф.; неизвестные a,b:![]()
![]()
![]()
![]()
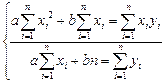 нормальная система. Из этой системы находим неизвес a,b и подставляем
в ф.y=ax+b.
нормальная система. Из этой системы находим неизвес a,b и подставляем
в ф.y=ax+b.
15 вопрос: Двойной интеграл. Основные понятия и
определения. При n =1![]() при n=2
при n=2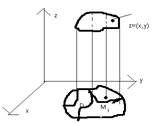 Область Д разобьем на n частей
произвольным образом. Получили n элементарных площадок Si(i=1,..,n).Внутри
каждой элементарной площадки выберем (.)ку Mi, найдем значение ф. z=f(x,y) в Mi f(Mi). Si даёт V цил.тела
с основанием Si, с высотой f(Mi). Составим интегральную сумму
Область Д разобьем на n частей
произвольным образом. Получили n элементарных площадок Si(i=1,..,n).Внутри
каждой элементарной площадки выберем (.)ку Mi, найдем значение ф. z=f(x,y) в Mi f(Mi). Si даёт V цил.тела
с основанием Si, с высотой f(Mi). Составим интегральную сумму![]() , тогда если
, тогда если![]() , то этот lim на-ют
двойным интегралом ф. z=f(x,y) по области Д. Этот lim не
зависит ни от способа разбиение обл. Д на элем площадки(.)Mi.
Теорема(«Необходимое условие интегрируемости ф. двух переменных»Если . z=f(x,y)
непрерывна в области Д, то (сущ.)
, то этот lim на-ют
двойным интегралом ф. z=f(x,y) по области Д. Этот lim не
зависит ни от способа разбиение обл. Д на элем площадки(.)Mi.
Теорема(«Необходимое условие интегрируемости ф. двух переменных»Если . z=f(x,y)
непрерывна в области Д, то (сущ.) ![]() , а значит и
двойной интеграл от f(x,y) по Д. Итак по определению
, а значит и
двойной интеграл от f(x,y) по Д. Итак по определению ![]()
16 вопрос: Свойство двойного интеграла:1.двойной интеграл от суммы 2ых интегралов от этих ф.
![]()
2)постоянный множитель
можно выносить за знак двойного интеграла:![]()
3)Если обл. Д разбита
на сумму 2ых областей, то двойной интеграл по обл Д равен сумме двойных
интегралов по обл Д1 и Д2![]() док-во:т.к. lim
интегральной суммы не зависит от способа разбиения обл Д,
док-во:т.к. lim
интегральной суммы не зависит от способа разбиения обл Д, 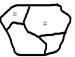 то будем разбивать её на элементарные площадки,
не пересекая границы обл. Д1, Д2; тогда
то будем разбивать её на элементарные площадки,
не пересекая границы обл. Д1, Д2; тогда ![]()
![]()
![]()
![]()
17 вопрос: Вычисление 2ого интеграла в декартовы координатах.т.к. lim не зависит от способа разбиения области Д на элементарной площадки, то будем её разбивать прямыми параллельными осями Ox,Oy:
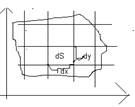 dS=dx*dy-элементарная
площадка. В декатовых координатах
dS=dx*dy-элементарная
площадка. В декатовых координатах ![]()
Если ф.z=f(x,y) непрерывна в области Д, то вычисление интеграла двойного сводится к выч. Двух кратного интеграла в случае правильности области Д. Д – правильной от Oy(в направлении Oy) , если она ограниченна прямыми y=y1(x),y=y2(x),т.е. имеет вид:
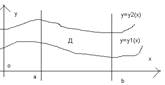
Д правильная оси Ox(в напр. Ox)y=c,y=d,x=x1(y),x=x2(y)
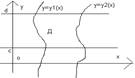
Область, правильная
отн Ox и Oy, на-ся правильной. Если Д- прав.отн Oy,то 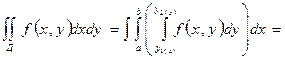
![]() интеграл
интеграл
![]() - внутренний интегралом.
- внутренний интегралом.![]() - внешним. Внутрен. Берётся по
переменной y в предположим, что x-const.Если Д правильная отн. Ox, то
- внешним. Внутрен. Берётся по
переменной y в предположим, что x-const.Если Д правильная отн. Ox, то
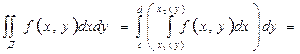
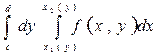
интеграл: ![]() - внутренним берётся в
предположении, что y=const.Замечание№1. Внешний интеграл всегда имеет
постоянные пределы интегрирования. Замечание№2 Если область не явл. Правильной
относительно Ox ,Oy, то надо её разбить на правильные подобласти и
использовать св-ва 3.Применение двойного интеграла к вычислению объемов и
площадей в декартовых координатах.
- внутренним берётся в
предположении, что y=const.Замечание№1. Внешний интеграл всегда имеет
постоянные пределы интегрирования. Замечание№2 Если область не явл. Правильной
относительно Ox ,Oy, то надо её разбить на правильные подобласти и
использовать св-ва 3.Применение двойного интеграла к вычислению объемов и
площадей в декартовых координатах.![]()
![]()
18 вопрос: Двойной интеграл в полярных координатах: В
общем случае, если в полярной системе координаты обл. Д, ограниченна кривыми ![]() ,
,![]() ,
лучами φ=α, φ=β, то она правильная:
,
лучами φ=α, φ=β, то она правильная:
![]()
Если Д неправильная
необходимо её разбить на правильные подобласти. Очень часто, когда обл.Д явл.
Кругом, частью круга, кольцом трудно вычислить двойной интеграл в декартовых
координатах. Требуется перейти в такую систему координат, чтобы интеграл
вычислялся произв-полярной системой координат. Формулы перехода из декартовой в
полярную:![]() Выведем формулы перехода к полярным
координатам в двойном интеграле; Теорема. Если z=f(x,y)
непрерывная. Обл. Д, x=x(u,v),y=y(u,v)-ф-ции переем u,v(криволинейных
координат), то
Выведем формулы перехода к полярным
координатам в двойном интеграле; Теорема. Если z=f(x,y)
непрерывная. Обл. Д, x=x(u,v),y=y(u,v)-ф-ции переем u,v(криволинейных
координат), то![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.