Градиент скалярного поля. Частные дифференциалы. Геометрический смысл. Двойной интеграл. Основные понятия и определения, страница 3

,где J-якобиан

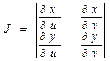применим эту теорему к полярной системе координатu→ρ,v→φ,J-?21 вопрос: Основные определения дифференциального уравнения. Дифференциальное Ур-ие – это Ур-ие, связывающие переменную, ф. и её производные. Если ф., входящая в дифференц. Ур-ие одной переменной, то оно наз-ся обыкновенным, если 2ых и более переменных, то оно на-ся – Ур-ие в частных производных. Общий вид д.у.

n-порядок Ур-ия; Если уравнение разрешается относительно n-ой производной, то Решить диффер Ур, значит найти такую ф.y(x), n-ая при подстановки в диффер Ур-ия обращает его в верное рав-во.

Дифференциальные уравнения: (1.)1.1уравн

Еия с разделяющими переменными; 1.2. однородные; 1.3. линейные, Бернулли;1.4.уравнения в полных дифференциалах; (2)2.1. Ур-ия, допускающие понижения порядка;2.2.ур-ия с постоянными коэффициентами и нулевой правой частью;2.3. Ур-ия с пост коэфф и правой частью спец и произвольного вида. Диффер Ур-ие 1  порядка F(x,y,z)=0:Если его можно разрешить относительно , то (1)- разрешённое относительно производной. Геометрически это уравнение  представляет поле направлений. Теорема(«Существование и единственности решения диффр  Ур-ия 1ого порядка»)Если f(x,y) непрерывна вместе с  в Д, содерж(.)(x0,y0), то существует единственное решение д.у. , удовлетворяющее нач. условиям y(x0)=y0(решение соотв. Задачи Коши без док-ва)

22 вопрос: уравненияс разделяющимипеременными имеют вид:(т.к. =, то это Ур-ие можно записать ).

Чтобы решить это Ур-ие, надо его почленно проинтегрировать, т.е.общее Ур-ие или общий интеграл Ур-ия. Ур-ие с разделяющими переменным делением на N1(y),M2(x): 

23 вопрос: Однородные Диффер Ур-ия 1 порядка. ф. z=f(x,y), на-ся однородной  n-го порядка, если  f(x,y). Дифф. Ур. Вида , назыв. Однородным, если f(x,y)- однор ф. n-ого порядка. Диффер. Ур. Вида явл. Однородным. Решение однородного Ур-ия с помощью замены переменной. ;

Замена переменной y=u*xчУр-ия с разделяющими переменнымиУр-ие с разделяющими переменными;

общий интеграл Ур-ия . Чтобы получить общий интеграл надо в полученный интеграл подставить .

24 вопрос: Линейные Диффер. Ур-ия 1 ого порядка. Л.д.у. 1ого порядка на-ся урав линейное, относительно ф. и её производной, т.е. Ур. Вида:существует два метода решения линейного Ур. 1-ого порядка.1. Метод Бернулли;2. Метод вариации произвольной постоянной; Уравнение Бернулли. Определение: Д.У. вида называется обобщённым линейным дифференциальным уравнением 1-ого порядка или уравнением Бернулли.

25 вопрос: У-ие Бернулли можно свести к линейному Ур-ию с помощью введения новой ф. . Покажем это. Разделим обе части Ур-ия Бернулли на ;, Пусть . Найдем , откуда.Подставляя  и  в Ур-ие , получим:. Умножив обе части Ур-ия на (1-n), получаем Ур-ие:, линейное, относительно z и . Это уравнение решаем с помощью подстановки Бернулли методом вариации произвольной постоянной как это было показано выше. Ур-ие Бернулли можно решать, как линейное, с помощью подстановки Бернулли . Метод вариации заключается в том, что сначала находят решение однородного Ур-ия , затем произвольную постоянную с находят как функцию  аргумента y, т.е. c=c(y).

26 вопрос: Дифференциальные Ур-ия в полных дифференциалах Определение вида: ,на-ся Диффер Ур-ем в полных дифференциалах, если его левая часть является полным дифференциалом некоторой ф.f(x,y). Другими словами Ур-ие (19) в полных дифферен можно записать в виде:. Теорема. Для того чтобы выражение , где ф. P(x;y);Q(x;y) и их частные производные непрерывны в некоторой области Д плоскости XOY, было полным дифференциалом некоторой ф., необходимо и достаточно, чтобы выполнялось условие:

27 вопрос: Дифференциальные Ур-ия высших порядков. Дифф n-ого порядка имеет вид: Если можно выразить , то Ур-ие (1) разрешенным отн-но n-ый производной. Решением Ур-ия (1), на-ся ф.y=φ(x), ко-ая при подстановке в Ур-ие обращает его в тождество. Общим решением Ур-ия (1) ,на-ся ф. , где , что : 1)  явл. Реш. (1); 2)(сущ.) ,, что ф.  удовл. Начал. Условиям : y(x0)=y0;; ф. , на-ся частным решением Ур-ем (1). Задачей Коши: Дифф Ур. N-ого порядка, на-ся задача о решение Ур.(1) с начальными условиями: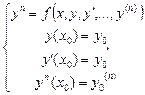

Теорема (сущ. И ед задачи Коши Ур.) Пусть  непрерывна вместе с частными производными 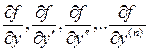 в некоторой области Д содержащей (.)ку , тогда в этой области !решение задачи Коши Ур(1). Если при решении Дифф. (1) не возможно получить выражение , то получают:- общий интеграл Ур.(1) или - частный интеграл Ур(1).