























ГЕНЕРИРОВАНИЕ И ОБРАБОТКА ДИНАМИЧЕСКИХ СИГНАЛОВ И
ВРЕМЕННЫХ РЯДОВ ДАННЫХ
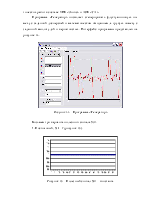
При сжатом описании регистрируемых сведений о работе объектов полезно использовать возможность представления сложных случайных элементов через более простые случайные элементы. Это соответствует свертыванию информации на основе моделей генерирования случайных величин и функций. В общем виде модель генератора представлена на рисунке 38.

Рисунок 38 – Общая модель генератора
Т.е. механизм генерирования случайных элементов представляется некоторой системой преобразующей базисные сигналы в выходные сигналы.
В роли базисных сигналов чаще всего используют одномерный или многомерный «белый шум».
Под последним понимают чисто случайный процесс, у которого отсутствуют всякие связи между соседними значениями. Этому процессу соответствуют с достаточной точностью флуктуации напряжения в сети, изменение ошибок регистрации параметров объектов, неточности работы механизмов при правильной наладке их и т.д.
С помощью преобразования белого шума можно представить очень многие стационарные и нестационарные случайные процессы. Такое представление положено в частности в теорию фильтрации и упреждения Калмана-Бьюси.
Модель генерирования выходных сигналов через преобразования одно и многомерного «белого шума» является полезной в деле идентификации металлургических объектов. А именно с помощью этой модели следует отображать эффекты влияния на реальные объекты неконтролируемых факторов, «прочих факторов».
Для, например, доменных печей эти эффекты соизмеримы с эффектами учитываемых факторов, поэтому очевидна необходимость их прямого математического описания с включением в модель объекта генератора эффектов прочих факторов. Для одномерного генератора можно использовать следующее соотношение:
x(i) = dx(i −1) +ε(i) где x(i) - выход генератора на i-ом такте x(i −1)- выход генератора на предыдущем такте (шаге, этапе, моменте) d - коэффициент авторегрессии, который определяется по автокорреляционной функции генерируемого сигнала.
ε(i)- базисный сигнал типа «белого шума».
Если эффекты прочих факторов для данного выхода объекта хорошо описываются экспоненциальной автокорреляционной функцией, то данное разностное уравнение является полностью адекватным. Это означает, что информация, содержащаяся в АКФ и в этом разностном уравнении, одинакова. Другими словами, свертывание информации о динамике анализируемых данных в форме АКФ и соответствующего генератора, эквивалентно.
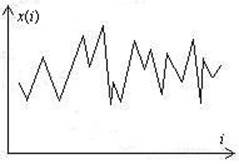
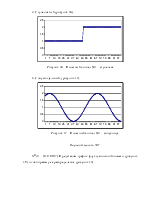
Рисунок 39 – Случайный процесс
На рисунке 39 показаны регистрируемые данные об изучаемом параметре x(i) . Количество этих данных может быть очень большим и достигать нескольких сотен или тысяч. Хранить и использовать такую информацию очень трудно. Естественно желание каким-то образом свернуть ее, сжать, представить в компактной форме. Для этого, как отмечалось, применяют гистограммы (рисунок 40), частотные распределения значений анализируемого параметра.
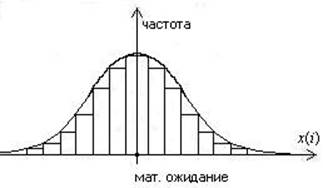
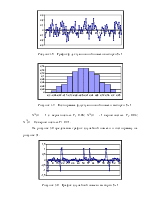
Рисунок 40 – Пример гистограммы
Недостаток сжатого описания с помощью гистограмм связан хотя бы с тем, что теряется информация о динамических связях между соседними значениями параметра. Отражение динамической связи, возможно АКФ, характеризует степень линейной связи между соседними отсчетами параметра.
Другой, марковской формой свертывания информации, является разностное уравнение x(i) = dx(i −1)+ε(i).
Марковская форма представления (описания) случайных процессов основывается на построении математической модели, связывающей будущие значения процесса со значениями его в настоящий момент времени и некоторые предшествующие моменты и значениями базисного сигнала в настоящий момент времени.
В разностном уравнении первого порядка значения x(i) в некоторый будущий момент времени i есть линейная функция от значенияx x(i–1) в настоящий момент времени и от значения белого шума ε(i) на интервале от настоящего момента (i–1) до будущего момента i.
Вопросами марковского представления случайных процессов занимается теория формирующих фильтров. Таким фильтром называется математическая модель или реальное устройство, преобразующее «белый» одно- или многомерный шум в случайный процесс с желаемыми статистическими свойствами.
Отдавая должное методам случайных процессов на основе формирующих фильтров, попытаемся подойти к свертыванию информации с точки зрения выделения и преобразования характерных кривых. Подчеркнем, что это не заменяет подхода формирующих фильтров, особенно при записи фильтров в разностных и дифференциальных уравнениях с использованием понятий пространство состояний, которые положены в основу теории фильтрации и предсказания Калмана-Бьюси и вообще теории управления стохастическими (вероятностными) системами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.