Каноническое представление можно получать также несколько иным путем, на основе заранее рассчитанной корреляционной функции ансамбля (множества) реализаций изучаемого процесса. Ансамбль – есть множество Т с заданной вероятностью появления.
В этом случае базисные функции могут задаваться не только из числа типовых функций, например, в виде многочленов, но и находиться применительно к фактической структуре конкретного процесса задаваемого множеством реализаций xl(t), l= 1,2,3...M . Множество, ансамбль реализаций принято обозначать символом {xl(t)}.
Получение базисных функций применительно к конкретной структуре процесса, если задана автокорреляционная функция его, можно производить в соответствии с разложением Карунена-Лоэва, конкретные варианты которого сводятся к использованию факторного анализа.
Подход на основе получения «своих» базисных функций для каждого конкретного процесса сопряжен с большими вычислительными трудностями, поэтому его следует применять только для тех важных практических задач, где непосредственный интерес представляет фактическая структура реализаций, а также необходимо обходиться минимальным числом членов разложения.
Метод наименьших квадратов и соответствующая ему система уравнений для оценки неизвестных коэффициентов лежит в основе вычислительных процедур (алгоритмов, программ) так называемого множественного корреляционного и регрессионного анализа. Поэтому, когда речь идет о названном аппарате, то его в вычислительном отношении можно соотносить с рассмотренным квадратичным критерием и вытекающей системой уравнений.
Расчеты по нахождению корреляционной и регрессионной зависимостей ведутся именно на этой основе, при использовании базисных функций, обычно в виде членов степенных полиномов, примененных к изменениям параметров, квадратам, производным и т. д.
Модель измерительного сигнала – это условное обозначение генерирующего абстрактного механизма, который может быть представлен следующей схемой (см. рисунок 42).
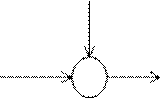
Рисунок 42 – Схема преобразующего механизма
Z(i) – сигнал измерительной информации; S(i) – полезная составляющая сигнала; N(i) – помеховая составляющая сигнала, N(i) = N0(i) + Nэ(i)
Математическая модель генерирования абстрактных равноточных измерений имеет следующий вид (см. рисунок 43).
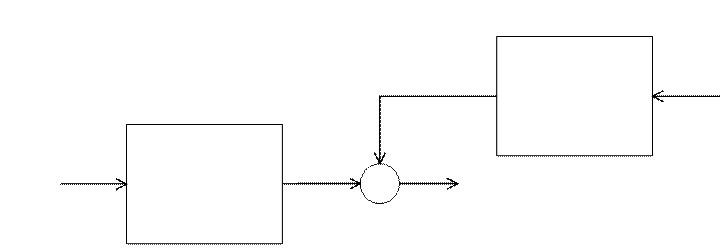
Рисунок 43 – Математическая модель генерирования абстрактных равноточных измерений
h(i) – порождающий сигнал, детерминированный входной сигнал
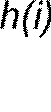
Наиболее информативным детерминированным сигналом является
ступенчатый или импульсный сигнал. Если входной сигнал отсутствует, то генерирование
(движение формирующего фильтра) осуществляется от начальных условий.
Полезная составляющая S(i) должна быть известна с точностью до конечного числа коэффициентов. Детерминированно-параметризованные модели полезного сигнала приведены в таблице 37.
Помеховая составляющая сигнала описывается преобразовательным механизмом вида N(i) =Φ[ε(i)], где ε(i) – модель параметризованной математической статистики, ε(i)∈H(0,σ); N(i) – нормальная гауссовская стационарная последовательность с нулевым (постоянным) математическим ожиданием и заданной дисперсией.
Основным условием для равноточных абстрактных измерений является неизменность преобразований (рисунок 43) в последовательности измерений, т.е. в зависимости от i. Это же условие относится к математическому ожиданию и дисперсии последовательности ( )ε i . Если Ф – пропорциональное звено, то в этом случае при независимых отсчетах ( )ε i независимы и нормальные отсчеты независимы и нормальные отсчеты N( )i .
Если преобразование Ф – динамическое, то N( )i – зависимые отсчеты, но это не мешает им быть равноточными в смысле обобщенного метода наименьших квадратов.
Неравноточные измерения имеют место во всех ситуациях, где не выполняются указанные условия, т.е. изменяются преобразования во времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.