Генерирование сигналов с заданными свойствами. Генерирование сигналов с заданными свойствами. Генерирование сигналов с заданными свойствами, страница 2

Теория формирующих фильтров и рассматриваемый ниже подход используют общую идею о выражении «сложных случайных элементов» через более простые случайные элементы. Простые случайные элементы можно называть базисными сигналами, т.е. сигналами, составляющими основу, базу, через которую получаются другие более сложные элементы.

В теории формирующих фильтров, как уже отмечалось в качестве базисных сигналов используют одно или многомерный белый шум. Многомерный, значит содержащий несколько составляющих, векторный шум, каждая компонента которого есть чисто-случайная последовательность. Схематически многомерный формирующий фильтр изображен на рисунке 41.

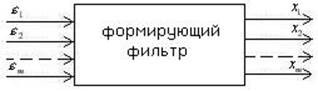
Рисунок 41 – Схема многомерного формирующего фильтра

где ε= ε₁,ε₂,...ε_m - многомерный, векторный белый шум с заданными дисперсиями и статистическими характеристиками взаимной связи между отдельными составляющими ε. Подчеркнем, что взаимная связь между компонентами белого шума может быть существенной, отсутствие связи предполагается в «белом шуме» только между последовательностью его значений. «Белость» предполагает собой, что нет связей временных, но коррелированность по компонентам ε₁ , ε₂ и т.д. может быть существенной, что следует учитывать.

x = x₁,x₂,...x_m  - многомерный генерируемый процесс, например, процесс измерения входных параметров доменной печи, процесс измерения эффектов «прочих факторов» (приведенные помехи к контролируемым выходным параметрам печи и т.д.).

Белый многомерный шум, при непрерывном или дискретном времени требует для задания алгоритма работы формирующих фильтров многомерных дифференциальных или разностных уравнений.

Отыскание этих уравнений для задач математического описания производственных процессов часто является очень трудным делом. Вполне возможно, что используя базисные сигналы другой природы, чем белый шум, можно получить более простые формы описания параметров реальных процессов. Конечно, при этом будет потеряна общность базисного сигнала, т.к. для каждого конкретного объекта и конкретной задачи потребуется определять свои базисные сигналы.

Конкретный подход к определению базисных сигналов используется в определенной мере в теории канонического представления случайных процессов, развитой в работах Пугачева В.С. Сущность этой теории заключается в том, что реализации случайного процесса представляются линейным разложением со случайными коэффициентами. Разложение производится по некоторым базисным функциям одного или нескольких аргументов. Эти базисные функции могут быть заданы в виде, например, одно или многомерных многочленов или определены по заданной корреляционной функции исследуемого процесса.

k

x_p (t) ≅∑c_j,lϕ_j (t)

j=1 t ∈[0,T]

где x_l (t)- конкретная l-тая реализация случайного процесса (изменение температуры t металла в ходе его нагрева). Областью определения каждой реализации является конечный интервал, длительностью T. Начало отсчетов всех реализаций условно обозначается моментом 0. Аргумент реализации t принадлежит ( ∈ ) конечной области [0, T].

Длина интервала T может устанавливаться равной длительности операции, например, нагрева металла в печи или плавки стали, а также принимается в связи с конкретной задачей, например, равной нескольким десяткам часов при математическом описании работы доменных печей.

ϕ_j (t) – базисные функции, в частности, члены степенного полинома

ϕ₁(t) = 1;

ϕ₂ (t) = t; ϕ₃(t) = t² и т.д. или тригонометрические функции, или функции определенные применительно к конкретному процессу, на основе автокорреляционной функции множества реализаций случайного процесса x_l(t), l= 1,2,3...M где M - количество реализаций. c_j,l – случайные весовые коэффициенты, определяемые для каждой реализации, например, по методу наименьших квадратов. Определение коэффициентов в соответствии с методом наименьших квадратов для каждой реализации изучаемого процесса и их последующее выражение согласно процедурам Трамм-Шмидта, компонентного и факторного анализов соответствует одному из вариантов канонического представления случайных процессов («канонис» – простой, каноническое разложение – разложение по простым случайным элементам, например, по заданным базисным функциям и некоррелируемым случайным величинам).