Генерирование сигналов с заданными свойствами. Генерирование сигналов с заданными свойствами. Генерирование сигналов с заданными свойствами, страница 4

Таблица 37 – Модели полезного сигнала

Вид	График	Название
S(i) = ao = const		Постоянный
S(i) = a0 + a1i		Линейный
S(i) = a0e−a1i		Экспоненциальный
S(i) = F{V(i)}		Модель косвенного измерения (регрес- сионного анализа)
S(i) = a0sinωi		Синусоида
Здесь a0,a1 – настроечные коэффициенты модели, i – дискретные моменты времени, i =1,2,...,n

1.1.3 Примеры генерирования сигналов и временных рядов данных

При различных исследовательских задачах, для сопоставления результатов сглаживания и получения достоверных оценок необходимо проведение экспериментов на нескольких выборках. Для генерации случайной помехи воспользуемся программой «Генератор» в составе подсистемы выполнения практических работ в составе УИК «Логос» и АОК «СА».

Программа «Генератор» позволяет сгенерировать флуктуационную помеху с заданной дисперсией и математическим ожиданием, а грубую помеху с заданной амплитудой и вероятностью. Интерфейс программы представлен на рисунке 44.

 

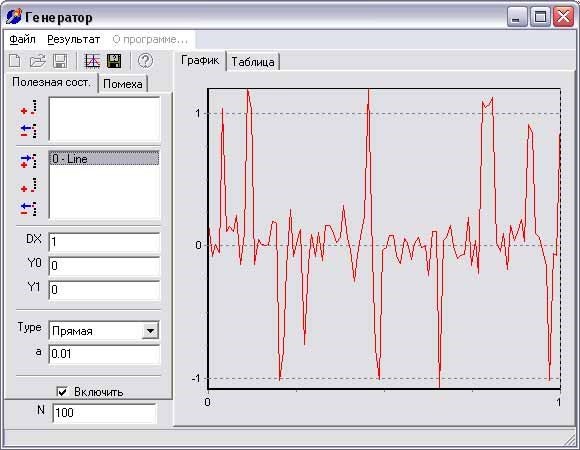
Рисунок 44 – Программа «Генератор»

Возьмем три варианта полезного сигнала S(i).

1.  Постоянный, S(i)=1 (рисунок 45).

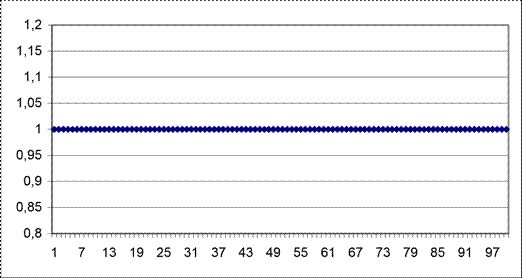
Рисунок 45 – Полезный сигнал S(i) – константа

2.  Ступенчатый(рисунок 46).

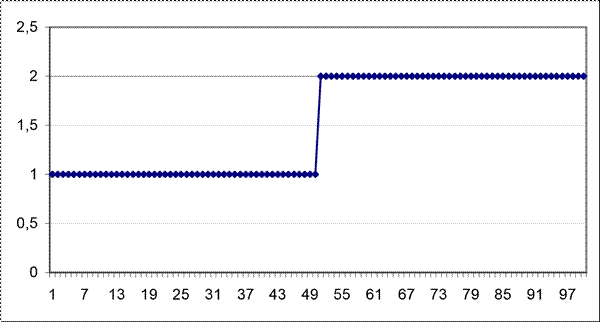
Рисунок 46 – Полезный сигнал S(i) – ступенька

3.  Синусоидальный, (рисунок 47).

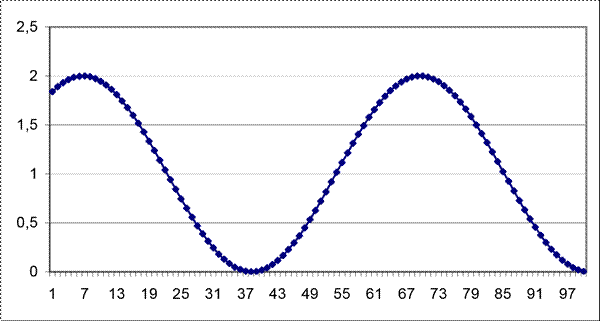
Рисунок 47 – Полезный сигнал S(i) – синусоида

Вариант помехи №1

N^Н(i) = [0, 0.0107]. Представим график флуктуационной помехи (рисунок 48) и гистограмму ее распределения (рисунок 49).

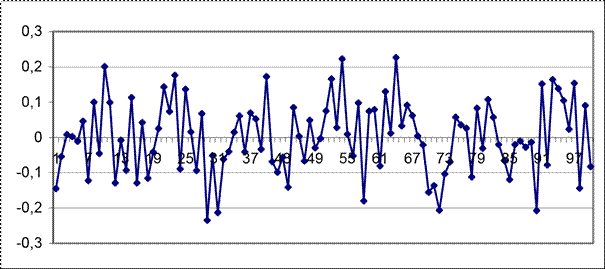
Рисунок 48 – График флуктуационной помехи выборки № 1

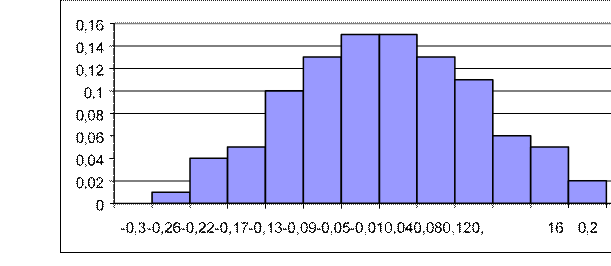
Рисунок 49 – Гистограмма флуктуационной помехи выборки № 1

N^Э(i) = 1 с вероятностью P₁=0.06; N^Э(i) = -1 вероятностью P₂=0.03;

N^Э(i) = 0 с вероятностью P₁=0.91.

На рисунке 50 представим график случайной помехи и гистограмму на рисунке 51.

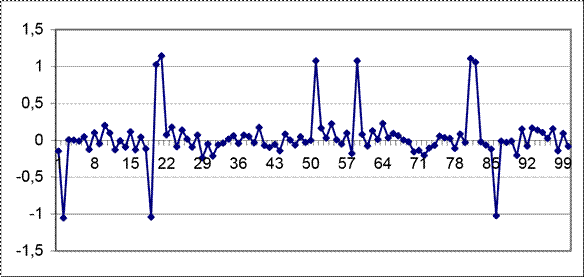
Рисунок 50 – График случайной помехи выборки № 1

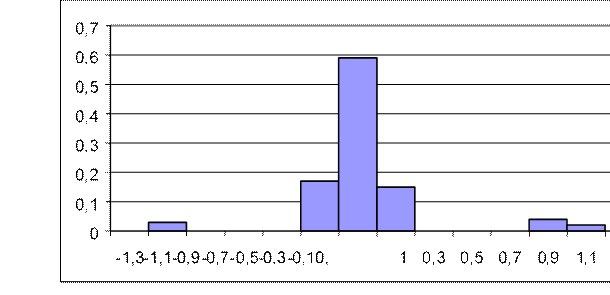
Рисунок 51 – Гистограмма случайной помехи выборки № 1

Вариант помехи № 2

N^Н(i) = [0, 0.0105]. Представим график флуктуационной помехи (рисунок

52) и гистограмму ее распределения (рисунок 53).

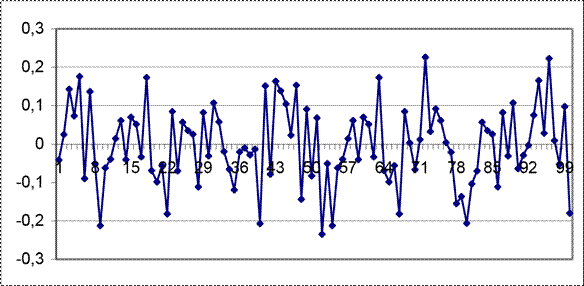
Рисунок 52 – График флуктуационной помехи выборки № 2

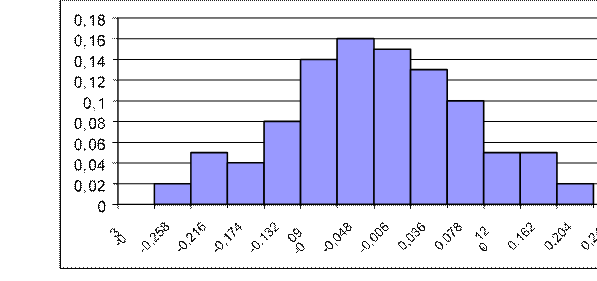
Рисунок 53 – Гистограмма флуктуационной помехи выборки № 2

N^Э(i) = 1 с вероятностью P₁=0.06; N^Э(i) = -1 вероятностью P₂=0.05;

N^Э(i) = 0 с вероятностью P₁=0.89.

На рисунке 54 представим график случайной помехи и гистограмму на рисунке 55.

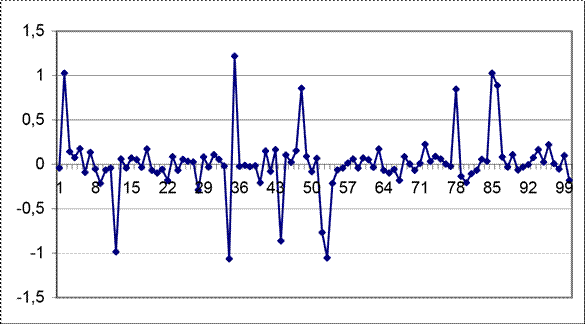
Рисунок 54 – График случайной помехи выборки № 2

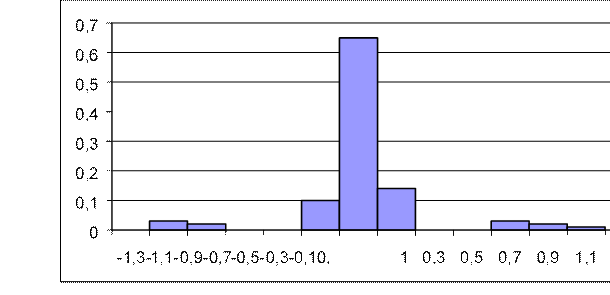
Рисунок 55 – Гистограмма случайной помехи выборки № 2

1.2 Обработка временных рядов данных

1.2.1 Операторы сглаживания

Рассматриваемые далее алгоритмы сглаживания записаны в ориентации на оценивание полезного сигнала и его производных в текущие i -ые отсчёты (дискретные моменты времени или циклы процесса). Тем самым, с использованием алгоритмов сглаживания в сущности решается задача фильтрации.

Традиционные алгоритмы сглаживания

Алгоритм скользящего среднего (СС). Формульное представление СС имеет вид:

                 ~         1       i

               Z( )i =  ^∑Z( )j ,                                                                       (1)

_M j=i−M+1

где M – число осредняемых данных.

Алгоритм экспоненциального сглаживания первого порядка (ЭСI). Формульное представление алгоритма ЭСI имеет вид:

~

Оценка начального значения Z(0) может определяться осреднением предыдущих N данных по алгоритму (1), т.е.

                     ~         ~                     ^ˆ(i) ,         ⎫⎪

Z(i) = Z(i −1)+α⋅∆Z

                                                  ^~                             ⎬                                                ⁽²⁾

∆Z^ˆ = Z(i)− Z(i −1) , i =1,2,....,⎪⎭

Для ЭС I настроечный параметр α(i) находится как постоянная величина из условия